Basic Principles

In this section we consider some of the basic commands of Mathematica(Wolfram, 1991) and how they can be used. We will make no attempt at completeness. Any work done using computer algebra will require a copy of the Mathematica handbook(Wolfram, 1991).

Note firstly the general point that the system is Case Sensitive: pi and Pi are different (the latter representing $\pi$). Different sorts of brackets are used for different purposes

()	for grouping	$(a+b)(a-b)$
[]	for functions	$f[x]$ or $Sin[x]$
{}	for lists	see examples later
[[]]	for indexing	$a[[n]] \equiv a_n$

In the examples to be given below prompts by the computer are shown in italics, things typed by the user in typewriter font and responses from the computer in normal type.

Variables are manipulated as in algebra unless they have been given a particular value:

In[1]:=	y = (1 + x)^2
Out[1]=	$${(1 + x)^2}$$
In[2]:=	x = 2
Out[2]=	$${2}$$
In[3]:=	y
Out[3]=	$${9}$$

As well as being given a permanent value variables can be given a temporary value

In[4]:=	Clear[x]
In[5]:=	y = (1 + x)^2
Out[5]=	$${(1 + x)^2}$$
In[6]:=	y/. x -> 2
Out[6]=	$${9}$$
In[7]:=	y
Out[7]=	$${(1 + x)^2}$$

Note the command Clear[x] which makes sure that x does not have a value.

Basic algebra can be done by using the functions Expand[] and Factor[] as follows

In[8]:=	Expand[y]
Out[8]=	$${1 + 2x + x^2}$$
In[9]:=	Factor[%]
Out[9]=	$${(1 + x)^2}$$

Note the use of % as shorthand for the result of the last operation. We could also have written Factor[Out[8]] here.

There are several other commands available which do specific manipulations on such expressions, in particular:

• Simplify[] tries to find the simplest form of an expression.
• Together[] put all terms over a common denominator.
• Collect[expr,x] groups together powers of x in the expression.
• Coefficient[expr,x^4] picks out the coefficient of x^4 in the expression.

Differentiation and integration are carried out using the D[f,x] and Integrate[f,x] operators.

In[10]:=	D[y,x]
Out[10]=	$${2(1+x)}$$
In[11]:=	Integrate[%,x]
Out[11]=	$${2x + x^2}$$
In[12]:=	Factor[%]
Out[12]=	$${x(2+x)}$$
In[13]:=	Integrate[y,x]
Out[13]=	$${x + x^2 + {x^3\over 3}}$$

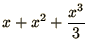or, using special functions,

In[14]:=	D[Sin[x],x]
Out[14]=	$${\mathop{\rm Cos}\nolimits [x]}$$
In[15]:=	Integrate[%,x]
Out[15]=	$${\mathop{\rm Sin}\nolimits [x]}$$
In[16]:=	x = Sin[z]
Out[16]=	$${\mathop{\rm Sin}\nolimits [z]}$$
In[17]:=	y
Out[17]=	$${(1 + \mathop{\rm Sin}\nolimits [z])^2}$$
In[18]:=	D[y,z]
Out[18]=	$${2\mathop{\rm Cos}\nolimits [z](1 + \mathop{\rm Sin}\nolimits [z])}$$
In[19]:=	Integrate[y,z]
Out[19]=	$${{3z\over 2} - 2\mathop{\rm Cos}\nolimits [z] - {\mathop{\rm Sin}\nolimits [2z]\over 4}}$$

Higher derivatives are written as

• D[f, x, y, z,...] multiple derivative ${\partial\over\partial x}{\partial\over\partial y}%% {\partial\over\partial z}\ldots$.
• D[f, {x,n}] repeated derivative ${\partial^n\over\partial x^n}$.

whereas definite integrals have the format

• Integrate[f, {x,a,b}] definite integral $\int_a^b \d x$.
• Integrate[f, {x,0,Infinity}] definite integral $\int_0^\infty \d x$.

Whereas differentiation always has a well-defined answer, sometimes Mathematica is unable to find an analytical result. In such cases the function N[] can be used to obtain a numerical result.

In[20]:=	Integrate[Sin[Sin[x]], {x,0,1}]
Out[20]=	$${\mathop{\rm Integrate}\nolimits [\mathop{\rm Sin}\nolimits [\mathop{\rm Sin}\nolimits [x]], \{x,0,1\}]}$$
In[21]:=	N[%]
Out[21]=	$${0.430606}$$
In[22]:=	N[%%,40]
Out[22]=	$${0.430606103120690604912377355248466}$$

where the last command evaluates the 2nd last (%%) result to 40 significant figures. This function can also be used in other situations such as

In[23]:=	N[Pi, 100]
Out[23]=	$${3.1415926535897932384626433832795028841971693993751}$$
	$05820974944592307816406286208998628034825342117068$

Mathematica has a number of built in constants (all beginning with capital letters) such as

In[24]:=	E^(I Pi)
Out[24]=	$${-1}$$