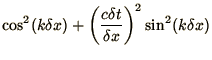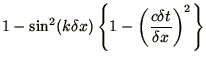Next: Non-Linear Equations
Up: Hyperbolic Equations
Previous: A Simple Algorithm
An Improved Algorithm -- the Lax method
We see from (2.20) that our simple method is in fact
unstable for the advection equation, for all finite values of 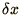 and
and 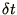 . How might we improve on this? Let us consider a minor
(?) modification of (2.11)
. How might we improve on this? Let us consider a minor
(?) modification of (2.11)
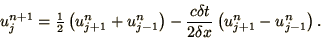 |
(2.21) |
in which the term in 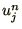 has been replaced by an average over its 2
neighbours.
When we apply the same (von Neumann) analysis to this algorithm
we find
has been replaced by an average over its 2
neighbours.
When we apply the same (von Neumann) analysis to this algorithm
we find
![\begin{displaymath}
v^{n+1} = \left[\cos(k \delta x)
- i{c\delta t\over\delta x}\sin(k \delta x)\right]v^n
\end{displaymath}](img198.png) |
(2.22) |
so that
which is stable for all 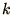 as long as
as long as
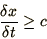 |
(2.25) |
which is an example of the Courant-Friedrichs-Lewy condition
applicable to hyperbolic equations.
There is a simple physical explanation of this condition: if we start
with the initial condition such that 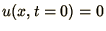 everywhere except at
one point on the spatial grid, then a point
everywhere except at
one point on the spatial grid, then a point 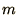 steps away on the grid
will remain zero until at least
steps away on the grid
will remain zero until at least 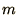 time steps later. If, however, the
equation is supposed to describe a physical phenomenon which travels
faster than that then something must go wrong. This is equivalent to the
condition that the time step,
time steps later. If, however, the
equation is supposed to describe a physical phenomenon which travels
faster than that then something must go wrong. This is equivalent to the
condition that the time step, 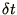 , must be smaller than the time
taken for the wave to travel the distance of the spatial step,
, must be smaller than the time
taken for the wave to travel the distance of the spatial step, 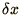 ; or that the speed of propagation of information on the grid,
; or that the speed of propagation of information on the grid,
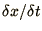 , must be greater than any other speed in the problem.
, must be greater than any other speed in the problem.



Next: Non-Linear Equations
Up: Hyperbolic Equations
Previous: A Simple Algorithm