


Next: Boundary Conditions
Up: Project Lagrangian
Previous: Project Lagrangian
The difference equations are,
where,
 |
(2.53) |
and,
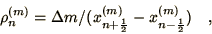 |
(2.54) |
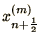 and
and
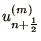 are the positions and
velocities of the cell boundaries.
are the positions and
velocities of the cell boundaries.
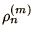 and
and 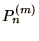 are the densities and pressures in the cells.
are the densities and pressures in the cells. 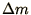 is the mass
in each cell.
It is useful for the purpose of programming to redefine things to get
rid of the various half integer indices. Hence we can write the
equations as
is the mass
in each cell.
It is useful for the purpose of programming to redefine things to get
rid of the various half integer indices. Hence we can write the
equations as
which maps more easily onto the arrays in a program.



Next: Boundary Conditions
Up: Project Lagrangian
Previous: Project Lagrangian