


Next: Iterative Methods
Up: Systems of Equations and
Previous: Systems of Equations and
Most library routines, for example those in the
NAG (Numerical Algorithms Group, n.d.) or LaPack (Lapack Numerical Library, n.d.)
libraries are based on some
variation of Gaussian elimination. The standard procedure is to call a
first function which performs an
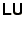 decomposition of the
matrix
decomposition of the
matrix 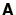 ,
,
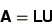 |
(3.10) |
where 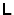 and
and 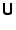 are lower and upper
triangular matrices respectively, followed by a function which
performs the operations
are lower and upper
triangular matrices respectively, followed by a function which
performs the operations
on each column of 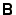 .
The procedure is sometimes described as Gaussian Elimination.
A common variation on this procedure is partial pivoting. This is
a trick to avoid numerical instability in the Gaussian Elimination (or
.
The procedure is sometimes described as Gaussian Elimination.
A common variation on this procedure is partial pivoting. This is
a trick to avoid numerical instability in the Gaussian Elimination (or
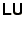 decomposition) by sorting the rows of
decomposition) by sorting the rows of 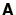 to
avoid dividing by small numbers.
There are several aspects of this procedure which should be noted:
to
avoid dividing by small numbers.
There are several aspects of this procedure which should be noted:
- The
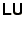 decomposition is usually done in
place, so that the matrix
decomposition is usually done in
place, so that the matrix 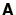 is overwritten by the matrices
is overwritten by the matrices
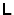 and
and 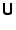 .
.
- The matrix
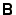 is often overwritten by the solution
is often overwritten by the solution
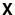 .
.
- A well written
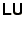 decomposition routine should be
able to spot when
decomposition routine should be
able to spot when 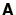 is singular and return a flag to tell you
so.
is singular and return a flag to tell you
so.
- Often the
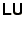 decomposition routine will also return
the determinant of
decomposition routine will also return
the determinant of 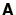 .
.
- Conventionally the lower triangular matrix
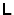 is defined
such that all its diagonal elements are unity. This is what makes it
possible to replace
is defined
such that all its diagonal elements are unity. This is what makes it
possible to replace 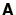 with both
with both 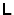 and
and 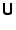 .
.
- Some libraries provide separate routines for the Gaussian
Elimination and the Back-Substitution steps. Often the
Back-Substitution must be run separately for each column of
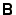 .
.
- Routines are provided for a wide range of different types of
matrices. The symmetry of the matrix is not often used however.
The time taken to solve 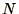 equations in
equations in 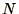 unknowns is generally
proportional to
unknowns is generally
proportional to 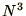 for the Gaussian-Elimination
(
for the Gaussian-Elimination
(
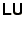 -decomposition) step. The Back-Substitution step
goes as
-decomposition) step. The Back-Substitution step
goes as 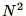 for each column of
for each column of 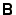 . As before this
may be modified by parallelism.
. As before this
may be modified by parallelism.



Next: Iterative Methods
Up: Systems of Equations and
Previous: Systems of Equations and