


Next: The Model
Up: Project Phonons
Previous: Introduction
The mathematical theory of Penrose tilings gets quite high
brow and abstruse, but everything is very simple in one
dimension. Then the two shapes are lines of different
lengths, which we shall call 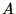 and
and 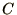 , for Adult and Child
(Fibonacci actually studied the dynamics of rabbit populations).
Every year each adult has one child and each child becomes an adult.
Let us start with a single child
, for Adult and Child
(Fibonacci actually studied the dynamics of rabbit populations).
Every year each adult has one child and each child becomes an adult.
Let us start with a single child
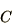 |
(3.40) |
and then repeatedly apply the ``generation rule,''
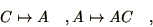 |
(3.41) |
to obtain longer and longer sequences. The first few
sequences generated are,
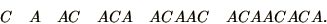 |
(3.42) |
Note the interesting property that each generation is the ``sum'' of the
2 previous generations: 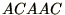 =
= 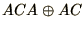
In a one dimensional Fibonacci quasicrystal, the longs and
shorts could represent the interatomic distances; or the strengths
of the bonds between the atoms; or which of two different types
of atom is at that position in the chain.



Next: The Model
Up: Project Phonons
Previous: Introduction