The Olami-Feder-Christensen Model of Earthquakes
The sandpile model of Bak, Tang, and Wiesenfeld displays self-organised
criticality due to an inherent conservation law of the dynamical variable.
However, there exists also slowly driven models which violate the
conservation law but nevertheless display the characteristic features of SOC:
after a transient, the size distribution of events is a power law with a
cutoff that diverges when the system size is increased.
The Olami-Feder-Christensen (OFC) model of a earthquake fault serve as an
example of such a nonconservative model.
The convective flow in the asthenosphere causes tectonic plates
to move relatively to one another causing strain to build up at
the boundary of the plates.
The lithosphere is so rigid that the strain
is released very suddenly through earthquakes. Thus the
worldwide occurrence of earthquakes outline the plate boundaries.
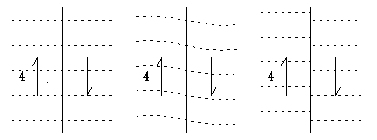
Figure 1: A simple model of the San Andreas fault. The single line is a symbol
for a transform fault. The (half) arrows show the direction
of the relative movement. The tectonic plates
move with a relative velocity of about 4 cm/year.
Strain builds up along the boundary of the plates. The
strain is released through an earthquake when the friction
cannot sustain the strain any more.
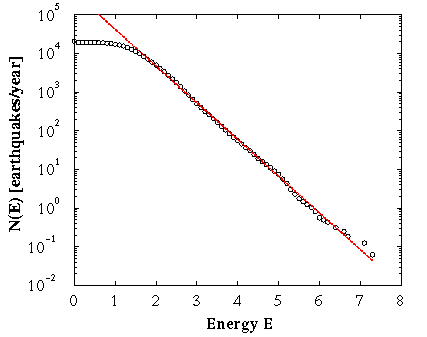
Figure 2: The number of earthquakes N(E) with energy release larger
than E per year (open circles).
The red dashed line is the Gutenberg-Richter
law Log10N(E) = -B Log10(E), B = 0.95.
The deficit at small
energy, is related to the problems with detecting small
earthquakes. The data approximates a power law over 5.5 orders of magnitude
in energy E and N(E). The data are from California during the
period 1984 - 2000.
In the model, the fault is represented by a two-dimensional network of blocks
interconnected by springs. Additionally, each block is connected to a
single rigid driving plate by another set of springs as well as
connected frictionally to a fixed rigid plate.
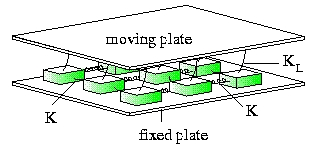
Figure 3: The geometry of the spring-block model. The force on the blocks increases uniformly as a response to the relative
movement of the tectonic plates. Strain builts up and is released
through an earthquake when the friction cannot sustain the strain any
more.
The blocks are driven by the relative movement of the two rigid
plates. When the force on one of the blocks is larger than some
threshold value Fth (the maximal static friction), the block
slips. We assume that the moving block slips to
the zero force position.
Slip of one block will redefine the forces
on its nearest neighbours. This may lead to instabilities of the
neighbouring blocks and thus, as a result, in further slips and
a chain reaction (earthquake) can evolve. The total number of
slips following a single initial slip event is a measure
of the size (seismic moment) of the earthquake.

Figure 4:
The probability P(E) of energy release E during an earthquakes
exhibits a power-law behaviour with a cutoff that increases with
system size L. Hence the model is critical despite the inherent
nonconservative nature and reproduces the observed Gutenberg
Richter law for the frequency of earthqukes versus size.
The origin of SOC in nonconservative models is conceptually
different from the origin of SOC in conservative models.
The main objective in future research is to understand the necessary
conditions under which critical scale invariant behaviour
occur spontaneously in weakly driven many-body systems.
SELECTED PUBLICATIONS
-
K. Christensen,
Self-Organization in Models of Sandpiles, Earthquakes, and Fireflies.
Ph.D. thesis, 1-131, University of Aarhus, Denmark (1992).
-
Z. Olami, H.J.S. Feder, and K. Christensen,
Self-Organized Criticality in a Continuous, Nonconservative Cellular Automaton Modeling Earthquakes.
Phys. Rev. Lett. 68, 1244-1247 (1992).
-
K. Christensen and Z. Olami,
Variation of the Gutenberg-Richter b Values and Nontrivial Temporal Correlations in a Spring-Block Model ...
J. Geophys. Res. 97, 8729-8735 (1992).
-
Z. Olami and K. Christensen,
Temporal Correrations, Universality, and Multifr
actality in Spring-Block Model of Earthquakes.
Phys. Rev. A 46, R1720-R1723 (1992).
-
K. Christensen and Z. Olami,
Scaling, Phase Transitions, and Nonuniversality
in a Self-Organized Critial Cellular-Automaton Model.
Phys. Rev. A 46, 1829-1838 (1992).
-
K. Christensen and Z. Olami,
Sandpile Models with and without an Underlying Spatial Structure.
Phys. Rev. E 48, 3361-3372 (1993).

From Yukon Ho!, a Calvin and Hobbes Collection by Bill Watterson, 1989.
[ Home ][ Research
interests ]





