
We show that rain events are analogous to a variety of nonequilibrium relaxational processes in Nature such as earthquakes and avalanches. By identifying rain events as the basic entities of the phenomenon, we find that the number density of rain events per year is inversely proportional to the released water column raised to the power 1.4. This is the rain-equivalent of the Gutenberg-Richter law for earthquakes and the scale-free distribution of avalanche sizes in slowly driven granular piles. The event durations and the waiting times between events are also characterised by scaling regions, where no typical time scales exist. In addition, the accumulated water column displays scale-free fluctuations. All of our findings are consistent with the concept of self-organised criticality, which refers to the tendency of slowly driven nonequilibrium systems to be poised at a critical state without the need of any fine tuning.
Rainfall and rainfall-related quantities have been recorded for centuries. All these measurements, however, have the disadvantage of low sensitivity and low temporal resolution. A time series from radar measurements of high precision rain rates with one minute resolution was analysed. The data were collected at the Baltic coast Zingst by the Max-Planck-Institute for Meteorology, Hamburg, Germany using a Micro Rain Radar MMR-2 developed by METEK. The data refer to a height range of 50 m at 250 m above sea level during the period January - July 1999. The detection threshold for rain rates under the pertinent operation parameters was qmin = 0.005 mm/h. Below this threshold, the rain rate q(t) = 0 by definition.

We define an event as a sequence of successive non-zero rain rates and the event size is defined as the released water column in mm, that is, the time-integral of the rain rate over an event.
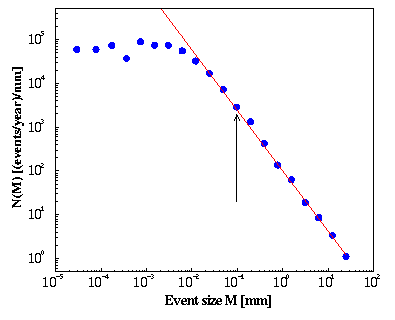
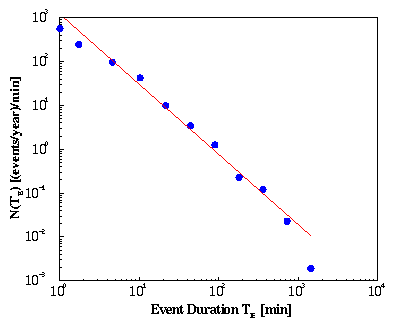
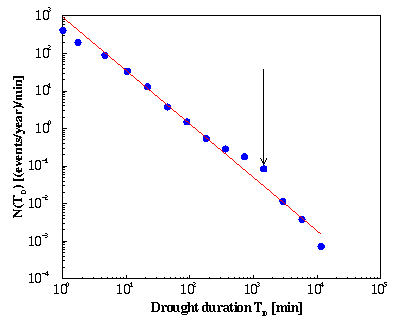
In summary, the rain event sizes and durations and the waiting times between events are characterised by scaling regions, where no typical size or time scale exist. The phenomenon of rain is scale free.
Self-organised criticality offers the appropriate framework for dealing with relaxational processes with burst-like behaviour whose statistics are determined by scale-free power laws. The term self-organised criticality refers to the tendency of many systems driven by an energy input at a slow and constant rate to enter states characterised by scale-free behaviour. The statistics of the systems then resemble those of equilibrium systems near the critical point of a phase transition.
A well-known example of such a process is the energy flow through the lithosphere, including the outermost crust of Earth. Tectonic plates are driven at a slow rate by currents in the asthenosphere, the liquid part below the lithosphere, which transports heat by currents. The energy transferred to the plates is intermediately stored in the form of tension until it is finally released in an earthquake. Earthquake statistics follow the Gutenberg-Richter power law that relates the seismic moment, a measure of the released energy, to the probability of such an earthquake. Rather than a typical size with exponentially fewer larger than smaller quakes, scale-free behaviour is observed.

Avalanches in a pile of grains might also display self-organised criticality: when grains are dropped onto a pile, one by one, the pile ultimately reaches a stationary critical state in which its slope fluctuates about a constant angle of repose, with each new grain being capable of inducing an avalanche on any of the relevant size scales.
| System | Atmosphere | Crust of Earth | Granular pile |
| Energy source | Sun | Convection | Adding grains |
| Energy storage | Vapour | Tension | Potential |
| Threshold | Saturation | Friction | Friction |
| Relaxation | Rain event | Earthquakes | Avalanches |
New insight into the working of rain can be gained by defining rain events, which can be regarded as energy relaxations similar to earthquakes or avalanches. Taking this perspective, scale-free power-law behaviour is found to govern the statistics of rain over a wide range of time scales and event size scales. Rainfall time series cannot be reproduced by conventional methods of probability theory. To enable anything more than an explicit reproduction of the scaling properties, a deeper understanding of self-organising processes leading to scale free behaviour must be sought. Our findings suggest that rain is an excellent example of a self-organised critical process. From the perspective of self-organised criticality, rain events do not look very different from earthquakes or avalanches. Rain events are relaxations in the sky.
SELECTED PUBLICATIONS