


Next: Some Ideas
Up: Project The
Previous: Project The
Consider a system of free electrons or of electrons in a semiconductor
within the effective mass approximation. Since the density of states
for free electrons,
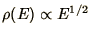 , the density of electrons,
, the density of electrons,
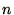 , below a chemical potential
, below a chemical potential 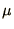 is
is
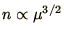 . If an
electrical potential energy,
. If an
electrical potential energy, 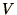 is added while keeping the
electrochemical potential energy (or Fermi level),
is added while keeping the
electrochemical potential energy (or Fermi level), 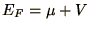 ,
constant, then the electron density changes to
,
constant, then the electron density changes to
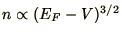 .
.
In the Thomas-Fermi approximation this charge density is assumed to
be a local quantity. Poisson's equation for the electrical potential
then takes the form
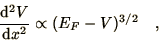 |
(5.1) |
which can be simplified into the form
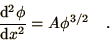 |
(5.2) |
This is a second order differential equation, so the general solution
must contain 2 unknowns. One solution is known, namely
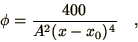 |
(5.3) |
which contains the single unknown  .
.
The object of the exercise here is to find a more general solution, or
at least something which may be used as such (i.e. a series expansion).



Next: Some Ideas
Up: Project The
Previous: Project The