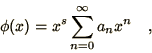Some Ideas

One possible approach would be to use the Frobenius method by assuming

$$\phi(x) = x^s\sum_{n=0}^\infty a_n x^n\quad,$$ (5.4)

but this presents 2 major difficulties.

• It doesn't adequately take account of the known solution, (5.3).
• The $3/2$ power cannot be easily expanded.

For this reason I suggest an alternative approach: make the substitution $\phi(x) = y^2(x)$ so that (5.2) then takes the form

$${\d^2 y^2\over\d x^2} = A y^3\quad,$$ (5.5)

and then use the Frobenius expansion in $z = x-x_0$ to solve the equation. Thus

$$y(z) = z^s\sum_{n=0}^\infty b_n z^n\quad.$$ (5.6)

By considering the limit of small $z$ and the known solution (5.3) we see immediately that $s = -2$ and that $b_0 = 20/A$.

You should try to find some more coefficients in the expansion (5.6) using Mathematica. The technique is similar to that described in the notes. You should bear in mind that we have already found one arbitrary coefficient, $x_0$, so that your solution should contain at least one other such arbitrary coefficient. Some of the coefficients may be zero; you should try to find a few non-trivial ones.

In your report you should describe how you have obtained the solution and any special insight you have gained into the nature of the solution. Instead of a program as an appendix you might consider including a printout of a Mathematica Notebook as well as some graphs of your solution.