


Next: The Diffusion Equation
Up: Conservative Methods
Previous: Conservative Methods
The Equation of Continuity
The archetypal example of a differential equation which implies a
conservation law is the equation of continuity, which, in its
differential form says that
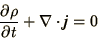 |
(2.33) |
where 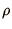 represents a density and
represents a density and 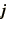 a current density. The density
and current density could be of mass, charge, energy or something else which is
conserved. Here we shall use the words charge and
current for convenience.
We consider here the 1D form for simplicity. The equation is derived by
considering space as divided into sections
of length
a current density. The density
and current density could be of mass, charge, energy or something else which is
conserved. Here we shall use the words charge and
current for convenience.
We consider here the 1D form for simplicity. The equation is derived by
considering space as divided into sections
of length 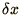 . The change in the total charge in a section is
equal to the total current coming in (going out) through its ends
. The change in the total charge in a section is
equal to the total current coming in (going out) through its ends
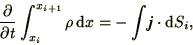 |
(2.34) |
It is therefore useful to re-express the differential equation in terms
of the total charge in the section and the total current coming in through each
face, so that we obtain a discrete equation of the form
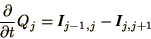 |
(2.35) |
where 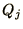 represents the total charge in part
represents the total charge in part 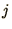 and
and
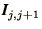 is the current through the boundary between parts
is the current through the boundary between parts 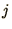 and
and 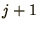 .
This takes care of the spatial part. What about the time derivative?
We can express the physics thus:
.
This takes care of the spatial part. What about the time derivative?
We can express the physics thus:
The change in the charge in a cube is equal to the
total charge which enters through its faces.



Next: The Diffusion Equation
Up: Conservative Methods
Previous: Conservative Methods