The Diffusion Equation

In many cases the current through a face is proportional to the difference in density (or total charge) between neighbouring cubes

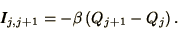$$\bi{I}_{j,j+1} = - \beta \left(Q_{j+1} - Q_j\right) .$$ (2.36)

Substituting this into the equation of continuity leads directly to the diffusion equation in discrete form

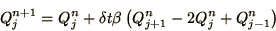$$Q_j^{n+1} = Q_j^n + \delta t\beta \left(Q_{j+1}^n - 2 Q_j^n + Q_{j-1}^n\right)$$ (2.37)

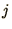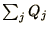which is of course our simple method of solution. To check whether this algorithm obeys the conservation law we sum over all $j$, as $\sum_j Q_j$ should be conserved. Note that it helps to consider the whole process as taking place on a circle as this avoids problems associated with currents across the boundaries. In this case (e.g.) $\sum_j Q_{j+1} = \sum_j Q_j$ and it is easy to see that the conservation law is obeyed for (2.37).