


Next: The Physics
Up: Project Lagrangian
Previous: Boundary Conditions
Sensible initial conditions might be,
where 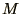 , the amplitude of the sound wave, is the ratio of
, the amplitude of the sound wave, is the ratio of 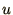 to the
sound speed (i.e. the Mach number). Be careful to choose sensible values
for the parameters: e.g. the values of
to the
sound speed (i.e. the Mach number). Be careful to choose sensible values
for the parameters: e.g. the values of 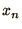 should rise monotonically
with
should rise monotonically
with 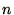 , otherwise some cells will have negative fluid densities.
The essential physics of the problem is independent of the absolute
values of the equilibrium pressure and density so you can set
, otherwise some cells will have negative fluid densities.
The essential physics of the problem is independent of the absolute
values of the equilibrium pressure and density so you can set  ,
,
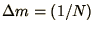 and
and
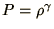 . In addition you can assume
that
. In addition you can assume
that
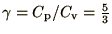 .
Note that the scheme is leap-frog but not of the dangerous
variety: alternate steps solve for
.
Note that the scheme is leap-frog but not of the dangerous
variety: alternate steps solve for 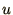 and
and  .
.