


Next: An Improvement?
Up: Project Lagrangian
Previous: Initial Conditions
Start with a relatively small value for
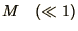 and show that
the wave maintains its shape and moves at the correct velocity. Then
increase
and show that
the wave maintains its shape and moves at the correct velocity. Then
increase 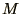 to find out what happens. The stability analysis for a
non-linear equation like this is difficult. Try halving the distance
between grid points. How does the behaviour of the system change? Do
the effects you observe describe real physics or are they numerical
artefacts?
One common numerical problem only manifests itself for large
to find out what happens. The stability analysis for a
non-linear equation like this is difficult. Try halving the distance
between grid points. How does the behaviour of the system change? Do
the effects you observe describe real physics or are they numerical
artefacts?
One common numerical problem only manifests itself for large 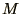 . Try
running for a few steps at
. Try
running for a few steps at 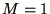 , look at the values for
, look at the values for  and try to
work out what has gone wrong. Think about how to prevent this problem
(Hint: you should find something very similar to the
Courant-Friedrichs-Lewy condition).
and try to
work out what has gone wrong. Think about how to prevent this problem
(Hint: you should find something very similar to the
Courant-Friedrichs-Lewy condition).