Introduction

The Korteweg de Vries equation,

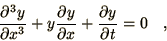$${\partial^3 y\over\partial x^3} + y{\partial y\over\partial x} + {\partial y\over\partial t} = 0\quad,$$ (2.61)

is one of a class of non-linear equations which have so-called soliton solutions. In this case a solution can be written in the form,

$$y = 12 \alpha^2 \mathop{\rm sech}\nolimits ^2\left[ \alpha (x - 4 \alpha^2 t)\right]\quad,$$ (2.62)

which has the form of a pulse which moves unchanged through the system. Ever since the phenomenon was first noted (on a canal in Scotland) it has been recognised in a wide range of different physical situations. The ``bore'' which occurs on certain rivers, notably the Severn, is one such. The dynamics of phase boundaries in various systems, such as domain boundaries in a ferromagnet, and some meteorological phenomena can also be described in terms of solitons.