


Next: Physics
Up: Project Solitons
Previous: Introduction
The simplest discretisation of (2.61), based on the Euler
method, gives the equation
![\begin{displaymath}
y_j^{(n+1)} = y_j^{(n)} - \left[{\mathchoice{{\textstyle{\f...
...1}^{(n)}
+ 2 y_{j-1}^{(n)} - y_{j-2}^{(n)}\right\}\right].
\end{displaymath}](img321.png) |
(2.63) |
You should check that this is indeed a sensible
discretisation of (2.61) but that it is unstable. Note that
when analysing the non-linear term in
(2.63) you should make the substitution
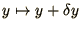 and retain the linear terms in
and retain the linear terms in 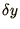 . Thereafter you should
treat
. Thereafter you should
treat 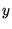 as a constant, independent of
as a constant, independent of 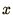 and
and 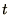 ,
and apply the von Neumann method to
,
and apply the von Neumann method to 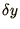 .
If you find the full stability analysis difficult you might consider
the 2 limits of large and small
.
If you find the full stability analysis difficult you might consider
the 2 limits of large and small 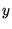 . In the former case the 3rd
derivative is negligible and (2.61) reduces to a non-linear
advection equation, whereas in the latter the non-linear term is
negligible and the equation is similar to the diffusion equation but
with a 3rd derivative. In any case you will require to choose
. In the former case the 3rd
derivative is negligible and (2.61) reduces to a non-linear
advection equation, whereas in the latter the non-linear term is
negligible and the equation is similar to the diffusion equation but
with a 3rd derivative. In any case you will require to choose 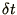 so that the equation is stable in both limits.
You are free to choose any method you wish to solve the equation but you
will find the Runge-Kutta or Predictor-Corrector methods most reliable. Hence treating
so that the equation is stable in both limits.
You are free to choose any method you wish to solve the equation but you
will find the Runge-Kutta or Predictor-Corrector methods most reliable. Hence treating
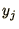 as a long vector
as a long vector 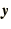 and the terms on the right-hand-side
of (2.63) as a vector function
and the terms on the right-hand-side
of (2.63) as a vector function
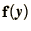 the R-K method can be written
concisely as
the R-K method can be written
concisely as
where
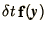 is the quantity in square brackets
is the quantity in square brackets ![$[]$](img51.png) in
(2.63).
Check that this method is stable, at least in the 2 limiting cases.
Bear in mind that the Runge-Kutta method is usable for oscillatory
equations in spite of the small instability as long as the term
in
(2.63).
Check that this method is stable, at least in the 2 limiting cases.
Bear in mind that the Runge-Kutta method is usable for oscillatory
equations in spite of the small instability as long as the term
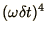 is small.
By studying the analytical solution (2.62) you should be able
to choose a sensible value for
is small.
By studying the analytical solution (2.62) you should be able
to choose a sensible value for 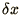 in terms of
in terms of 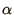 and from
the stability conditions you can deduce an appropriate
and from
the stability conditions you can deduce an appropriate 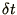 .
Again, by looking at (2.62) you should be able to decide on a
sensible size for the total system.
You should use periodic boundary conditions, so that your solitons can
run around your system several times if necessary. The easiest way to
do this is by using ``ghost'' elements at each end of your arrays.
Suppose your arrays should run from
.
Again, by looking at (2.62) you should be able to decide on a
sensible size for the total system.
You should use periodic boundary conditions, so that your solitons can
run around your system several times if necessary. The easiest way to
do this is by using ``ghost'' elements at each end of your arrays.
Suppose your arrays should run from 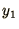 to
to 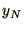 . Then you can add a
couple of extra elements to each end:
. Then you can add a
couple of extra elements to each end:
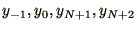 .
After each step you can then assign these values as
.
After each step you can then assign these values as
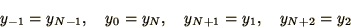 |
(2.66) |
so that the derivative terms in (2.63) can be calculated
without having to take any special measures.



Next: Physics
Up: Project Solitons
Previous: Introduction