


Next: Simple Matrix Problems
Up: Matrix Algebra
Previous: Introduction
There are several ways of classifying matrices depending on symmetry,
sparsity etc. Here we provide a list of types of matrices and the
situation in which they may arise in physics.
- Hermitian Matrices:
Many Hamiltonians have this property especially those containing
magnetic fields:
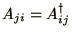 where at least some elements
are complex.
where at least some elements
are complex.
- Real Symmetric Matrices:
These are the commonest matrices in physics as most Hamiltonians can be
represented this way:
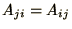 and all
and all 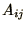 are real.
This is a special case of Hermitian matrices.
are real.
This is a special case of Hermitian matrices.
- Positive Definite Matrices:
A special sort of Hermitian matrix in which all the eigenvalues are
positive. The overlap matrices used in tight-binding electronic
structure calculations are like this.
Sometimes matrices are non-negative definite and zero
eigenvalues are also allowed. An example is the dynamical matrix
describing vibrations of the atoms of a molecule or crystal, where
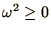 .
.
- Unitary Matrices:
The product of the matrix and its Hermitian conjugate is a unit matrix,
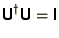 . A matrix whose columns are the
eigenvectors of a Hermitian matrix is unitary; the unitarity is a
consequence of the orthogonality of the eigenvectors. A scattering
(
. A matrix whose columns are the
eigenvectors of a Hermitian matrix is unitary; the unitarity is a
consequence of the orthogonality of the eigenvectors. A scattering
( ) matrix is unitary; in this case a consequence of current
conservation.
) matrix is unitary; in this case a consequence of current
conservation.
- Diagonal Matrices:
All matrix elements are zero except the diagonal elements,
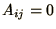 when
when 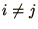 . The matrix of eigenvalues of a matrix has this form.
Finding the eigenvalues is equivalent to diagonalisation.
. The matrix of eigenvalues of a matrix has this form.
Finding the eigenvalues is equivalent to diagonalisation.
- Tridiagonal Matrices:
All matrix elements are zero except the diagonal and first off diagonal
elements,
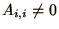 ,
,
 . Such matrices often
occur in 1 dimensional problems and at an intermediate stage in the
process of diagonalisation.
. Such matrices often
occur in 1 dimensional problems and at an intermediate stage in the
process of diagonalisation.
- Upper and Lower Triangular Matrices:
In Upper Triangular Matrices all the matrix elements below the
diagonal are zero,
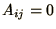 for
for 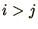 . A Lower Triangular Matrix is
the other way round,
. A Lower Triangular Matrix is
the other way round, 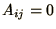 for
for 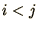 . These occur at an
intermediate stage in solving systems of equations and inverting
matrices.
. These occur at an
intermediate stage in solving systems of equations and inverting
matrices.
- Sparse Matrices:
Matrices in which most of the elements are zero according to some
pattern. In general sparsity is only useful if the number of non-zero
matrix elements of an
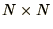 matrix is proportional to
matrix is proportional to 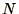 rather
than
rather
than 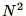 . In this case it may be possible to write a function which
will multiply a given vector
. In this case it may be possible to write a function which
will multiply a given vector 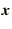 by the matrix
by the matrix 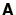 to give
to give
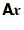 without ever having to store all the elements of
without ever having to store all the elements of
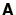 . Such matrices commonly occur as a result of simple
discretisation of partial differential equations, and in simple models
to describe many physical phenomena.
. Such matrices commonly occur as a result of simple
discretisation of partial differential equations, and in simple models
to describe many physical phenomena.
- General Matrices:
Any matrix which doesn't fit into any of the above categories,
especially non-square matrices.
There are a few extra types which arise less often:



Next: Simple Matrix Problems
Up: Matrix Algebra
Previous: Introduction