


Next: Types of Matrices
Up: Matrix Algebra
Previous: Matrix Algebra
Nearly every scientific problem which is solvable on a computer can be
represented by matrices. However the ease of solution can depend
crucially on the types of matrices involved. There are 3 main classes
of problems which we might want to solve:
- Trivial Algebraic Manipulation such as addition,
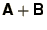 or multiplication,
or multiplication,
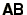 , of matrices.
, of matrices.
- Systems of equations:
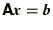 where
where 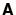 and
and 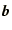 are known and we have to find
are known and we have to find 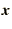 . This also
includes the case of finding the inverse,
. This also
includes the case of finding the inverse, 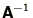 . The standard
example of such a problem is
Poisson's Equation.
. The standard
example of such a problem is
Poisson's Equation.
- Eigenvalue Problems:
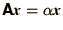 . This
also includes the generalised eigenvalue problem:
. This
also includes the generalised eigenvalue problem:
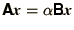 . Here we will consider the
time-independent Schrödinger equation.
. Here we will consider the
time-independent Schrödinger equation.
In most cases there is no point in writing your own routine to solve
such problems. There are many computer libraries, such as
Numerical Algorithms Group (n.d.), Lapack Numerical Library (n.d.)
(for linear algebra problems and eigenvalue problems).
which contain well tried routines. In addition
vendors of machines with specialised architectures often provide
libraries of such routines as part of the basic software.