


Next: Multiplication of Matrices
Up: Simple Matrix Problems
Previous: Simple Matrix Problems
In programming routines to add or subtract matrices it pays to remember
how the matrix is stored in the computer. Unfortunately this varies from
language to language: in C(++) and Pascal the first index varies slowest
and the matrix is stored one complete row after another; whereas
in FORTRAN the first index varies fastest and the matrix is stored one
complete column after another. It is generally most efficient to
access the matrix elements in the order in which they are stored. Hence
the simple matrix algebra,
 , should be
written in C3.1 as
, should be
written in C3.1 as
const int N =??;
int i, j;
double A[N][N], B[N][N], C[N][N];
for( i = 0; i < N; i++)
for( j = 0; j < N; j++)
A[i][j] = B[i][j] + C[i][j];
or its equivalent using pointers. In FORTRAN90 this should be written
integer :: i,j
integer, parameter :: N = ??
real, double precision :: A(N,N), B(N,N), C(N,N)
do i = 1,N
do j=1,N
A(j,i) = B(j,i) + C(j,i)
end do
end do
Note the different ordering of the loops in these 2 examples.
This is intended to optimise the order in which the matrix elements are
accessed. It is perhaps worth noting at this stage that in both
C++ and FORTRAN90 it is possible to define matrix type variables (classes) so that
the programs could be reduced to
matrix A(N,N), B(N,N), C(N,N);
A = B + C;
The time taken to add or subtract 2 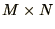 matrices is generally
proportional to the total number of matrix elements,
matrices is generally
proportional to the total number of matrix elements, 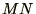 , although this
may be modified by parallel architecture.
, although this
may be modified by parallel architecture.



Next: Multiplication of Matrices
Up: Simple Matrix Problems
Previous: Simple Matrix Problems