


Next: Elliptic Equations
Up: Simple Matrix Problems
Previous: Addition and Subtraction
Unlike addition and subtraction of matrices it is difficult to give a
general machine independent rule for the optimum algorithm for
the operation. In fact matrix multiplication is a classic example of an
operation which is very dependent on the details of the
architecture
of the
machine. We quote here a general purpose example but it should be noted
that this does not necessarily represent the optimum ordering of the
loops.
const int L = ??, M = ??, N = ??;
int i, j, k;
double A[L][N], B[L][M], C[M][N], sum;
for ( j = 0; j < N; i++)
for ( i = 0; i < L; j++)
{
for ( sum = 0, k = 0; k < M; k++)
sum += B[i][k] * C[k][j];
A[i][j] = sum;
}
in C.
The time taken to multiply 2 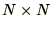 matrices is generally
proportional to
matrices is generally
proportional to 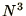 , although this
may be modified by
parallel processing.
, although this
may be modified by
parallel processing.