


Next: 2 or more Dimensions
Up: Elliptic Equations
Previous: Elliptic Equations
We start by considering the one dimensional Poisson's equation
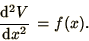 |
(3.2) |
The 2nd derivative may be discretised in the usual way
to give
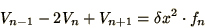 |
(3.3) |
where we define
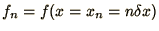 .
.
The boundary conditions are usually of the form 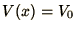 at
at
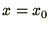 and
and
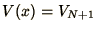 at
at 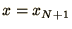 , although sometimes
the condition is on the first derivative. Since
, although sometimes
the condition is on the first derivative. Since 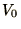 and
and 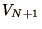 are both known the
are both known the 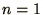 and
and 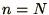 equations (3.3) may be
written as
equations (3.3) may be
written as
This may seem trivial but it maintains the convention that all the terms
on the left contain unknowns and everything on the right is known. It
also allows us to rewrite the (3.3) in matrix form as
![\begin{displaymath}
\left[\begin{array}{llllllll}
-2 &1 & & & & & & \\
1 &-2 &1...
...ot f_{N-1}\\
\delta x^2\cdot f_N - V_{N+1}
\end{array}\right]
\end{displaymath}](img382.png) |
(3.6) |
which is a simple matrix equation of the form
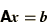 |
(3.7) |
in which 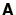 is tridiagonal. Such equations can be solved by
methods which we shall consider below. For the
moment it should suffice to note that the tridiagonal form can be solved
particularly efficiently and that
is tridiagonal. Such equations can be solved by
methods which we shall consider below. For the
moment it should suffice to note that the tridiagonal form can be solved
particularly efficiently and that functions
for this purpose can be found in most libraries of numerical functions.
There are several points which are worthy of note.
- We could only write the equation in this matrix form because the
boundary conditions allowed us to eliminate a term from the 1st and last
lines.
- Periodic boundary conditions, such as
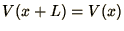 can be
implemented, but they have the effect of adding a non-zero element to the
top right and bottom left of the matrix,
can be
implemented, but they have the effect of adding a non-zero element to the
top right and bottom left of the matrix, 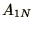 and
and 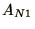 , so that
the tridiagonal form is lost.
, so that
the tridiagonal form is lost.
- It is sometimes more efficient to solve Poisson's or Laplace's equation
using Fast Fourier Transformation (FFT). Again there are efficient
library routines available (Numerical Algorithms Group, n.d.).
This is
especially true in machines with vector processors.



Next: 2 or more Dimensions
Up: Elliptic Equations
Previous: Elliptic Equations
![]() at
at
![]() and
and
![]() at
at ![]() , although sometimes
the condition is on the first derivative. Since
, although sometimes
the condition is on the first derivative. Since ![]() and
and ![]() are both known the
are both known the ![]() and
and ![]() equations (3.3) may be
written as
equations (3.3) may be
written as