


Next: Project Phonons
Up: Project Oscillations
Previous: Project Oscillations
The difference equations for the oscillating wire can be derived
by dividing it into N segments (10 or 20 should be sufficient)
each of which can be considered rigid. This would be the
case if the wire consisted of a series of rods connected
together.
Let  be the displacement of the bottom of the
be the displacement of the bottom of the 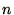 th
segment. Let
th
segment. Let 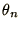 be the angle it makes with the
vertical. Let
be the angle it makes with the
vertical. Let 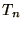 be the tension in the
be the tension in the 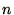 th segment.
Assume that the mass of the wire is located at the joints
of the segments,
th segment.
Assume that the mass of the wire is located at the joints
of the segments, 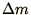 at each joint.
at each joint.
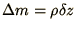 where
where 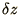 is
the length of each segment, and
is
the length of each segment, and 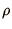 is the mass per
unit length of the wire. The equation of motion for
the mass at the bottom of the nth segment is,
is the mass per
unit length of the wire. The equation of motion for
the mass at the bottom of the nth segment is,
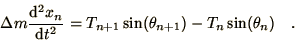 |
(3.33) |
Assume small oscillations so that
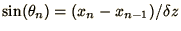 .
.
![\begin{displaymath}
\Delta m \frac{\d^{2}x_{n}}{\d t^{2}} =
\frac{1}{\delta z...
... -
( T_{n+1} + T_{n} ) x_{n} + T_{n} x_{n-1} \right] \quad .
\end{displaymath}](img488.png) |
(3.34) |
The mass associated with the end of the wire will be only
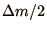 since there is no contribution from the
(N+1)th segment. Consequently, the equation of motion for
this point is,
since there is no contribution from the
(N+1)th segment. Consequently, the equation of motion for
this point is,
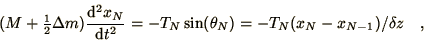 |
(3.35) |
where 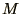 is any mass carried by the crane. In addition the displacement
of the top of the wire is zero, so that
is any mass carried by the crane. In addition the displacement
of the top of the wire is zero, so that 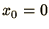 in the equation for
in the equation for
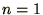 .
.
The modes of oscillation are calculated by seeking solutions
of the form
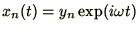 . Substituting
this into the equations of motion gives,
. Substituting
this into the equations of motion gives,
The specification of the equations is completed by noting that, from
the equilibrium conditions,
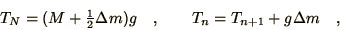 |
(3.38) |
where 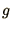 is the acceleration due to gravity.
is the acceleration due to gravity.
The equations can be organised in the form,
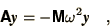 |
(3.39) |
where 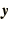 is the column vector of displacements,
is the column vector of displacements,
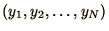 ,
, 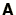 is a symmetric tridiagonal matrix and
is a symmetric tridiagonal matrix and
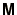 is a diagonal matrix. The problem becomes one of finding the
eigenvalues,
is a diagonal matrix. The problem becomes one of finding the
eigenvalues, 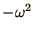 , and eigenvectors,
, and eigenvectors, 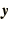 , of a generalised
eigenvalue problem. The eigenvectors show how the wire distorts when
oscillating in each mode and the eigenvalues give the corresponding
oscillation frequencies. Low frequency modes are more important than
high frequency modes to the crane manufacturer.
, of a generalised
eigenvalue problem. The eigenvectors show how the wire distorts when
oscillating in each mode and the eigenvalues give the corresponding
oscillation frequencies. Low frequency modes are more important than
high frequency modes to the crane manufacturer.
The problem can be solved most easily by using a LaPack routine which
finds the eigenvalues and eigenvectors directly.
However, before doing so it is necessary to eliminate the matrix
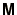 using the same method as discussed in problem 6.
using the same method as discussed in problem 6.
You should investigate both the computational aspects, such as the
dependence of the results on 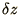 , as well as the physical ones,
such as the dependence of the behaviour on the mass,
, as well as the physical ones,
such as the dependence of the behaviour on the mass, 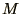 . Do your
results make physical sense? You might even compare them with a simple
experiment involving a weight on the end of a string.
. Do your
results make physical sense? You might even compare them with a simple
experiment involving a weight on the end of a string.



Next: Project Phonons
Up: Project Oscillations
Previous: Project Oscillations
![]() be the displacement of the bottom of the
be the displacement of the bottom of the ![]() th
segment. Let
th
segment. Let ![]() be the angle it makes with the
vertical. Let
be the angle it makes with the
vertical. Let ![]() be the tension in the
be the tension in the ![]() th segment.
Assume that the mass of the wire is located at the joints
of the segments,
th segment.
Assume that the mass of the wire is located at the joints
of the segments, ![]() at each joint.
at each joint.
![]() where
where ![]() is
the length of each segment, and
is
the length of each segment, and ![]() is the mass per
unit length of the wire. The equation of motion for
the mass at the bottom of the nth segment is,
is the mass per
unit length of the wire. The equation of motion for
the mass at the bottom of the nth segment is,
![]() . Substituting
this into the equations of motion gives,
. Substituting
this into the equations of motion gives,
![]() using the same method as discussed in problem 6.
using the same method as discussed in problem 6.
![]() , as well as the physical ones,
such as the dependence of the behaviour on the mass,
, as well as the physical ones,
such as the dependence of the behaviour on the mass, ![]() . Do your
results make physical sense? You might even compare them with a simple
experiment involving a weight on the end of a string.
. Do your
results make physical sense? You might even compare them with a simple
experiment involving a weight on the end of a string.