


Next: Project Oscillations
Up: Matrix Algebra
Previous: Sparse Matrices and the
Problems
- Poisson's equation
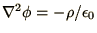 is usually differenced in 2 dimensions as
is usually differenced in 2 dimensions as
where
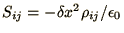 and
and
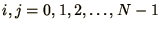 .
The difference equation can be written as a matrix equation
.
The difference equation can be written as a matrix equation
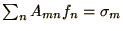 where
where
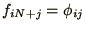 and
and
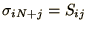 .
Write down the matrix
.
Write down the matrix 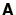 for
for 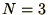 . Assume the boundaries are at
zero potential, i.e.
. Assume the boundaries are at
zero potential, i.e. 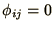 iff
iff
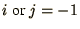 or
or
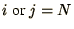 .
.
- The equation in question 1 can be solved
by the Gauss-Seidel method. If
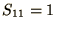 and
and 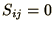 otherwise,
find
otherwise,
find
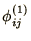 and
and
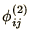 if
if
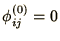 for
all
for
all 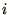 and
and 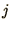 , where
, where
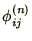 is the value of
is the value of 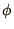 after
after
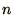 iterations.
iterations.
- Work out the factors, L and U, in the LU decomposition
of the matrix,
Hence,
- Solve the simultaneous equations,
for a variety of right hand sides, 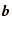 .
.
- Evaluate

- Find
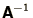
- Show that the Jacobi method (3.14) is
stable as long as,
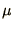 , the eigenvalue of largest modulus of
, the eigenvalue of largest modulus of
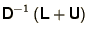 is less than unity.
is less than unity.
- Find both eigenvalues and the corresponding
left and right handed eigenvectors of the matrix
- The vibrational modes of a certain molecule are
described by an equation of motion in the form
where  and
and 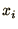 are the mass and the displacement respectively
of the
are the mass and the displacement respectively
of the 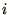 th atom and the real symmetric matrix
th atom and the real symmetric matrix 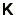 describes the
interactions between the atoms.
Show that this problem can be represented in the form of a generalised
eigenvalue problem:
describes the
interactions between the atoms.
Show that this problem can be represented in the form of a generalised
eigenvalue problem:
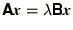 in which the
matrix
in which the
matrix 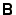 is positive definite.
By considering the transformation
is positive definite.
By considering the transformation
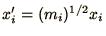 , show how to
transform this into a simple eigenvalue problem in which the matrix is
real symmetric.
, show how to
transform this into a simple eigenvalue problem in which the matrix is
real symmetric.
- Write down the types of matrices which occur in the
following problems:
- A simple discretisation (as in question1) of Poisson's
equation in 1 dimension.
- The same but in more than 1D.
- A simple discretisation (as above) of Schrödinger's equation
in 3 dimensions.
- Schrödinger's equation for a molecule written in terms of atomic basis
functions.
- Schrödinger's equation for a crystal at a general
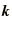 point in the Brillouin zone.
point in the Brillouin zone.



Next: Project Oscillations
Up: Matrix Algebra
Previous: Sparse Matrices and the
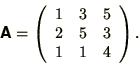
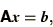
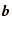 .
.

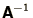
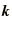 point in the Brillouin zone.
point in the Brillouin zone.