


Next: The Metropolis Algorithm
Up: Monte Carlo Methods and
Previous: Random Number Generators
Monte-Carlo Integration
Often we are faced with integrals which cannot be done analytically.
Especially in the case of multidimensional integrals the simplest
methods of discretisation can become prohibitively expensive. For
example, the error in a trapezium rule calculation of a 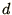 -dimensional
integral falls as
-dimensional
integral falls as 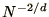 , where
, where 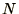 is the number of different
values of the integrand used. In a Monte-Carlo calculation the error
falls as
is the number of different
values of the integrand used. In a Monte-Carlo calculation the error
falls as  independently of the dimension. Hence for
independently of the dimension. Hence for 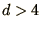 Monte-Carlo integration will usually converge faster.
Monte-Carlo integration will usually converge faster.
We consider the expression for the average of a statistic,
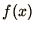 when
when  is a random number distributed according to a distribution
is a random number distributed according to a distribution 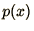 , then
, then
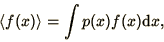 |
(4.6) |
which is just a generalisation of the well known results for (e.g. )
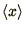 or
or
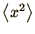 , where we are using the notation
, where we are using the notation
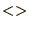 to denote averaging.
Now consider an integral of the sort which might arise while using
Laplace transforms.
to denote averaging.
Now consider an integral of the sort which might arise while using
Laplace transforms.
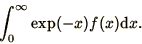 |
(4.7) |
This integral can
be evaluated by generating a set of 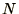 random numbers,
random numbers,
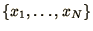 , from a Poisson
distribution,
, from a Poisson
distribution,
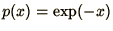 , and calculating the mean of
, and calculating the mean of 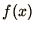 as
as
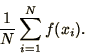 |
(4.8) |
The error in this mean is evaluated as usual by considering the
corresponding standard error of the mean
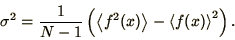 |
(4.9) |
As mentioned earlier, Monte-Carlo integration can be particularly efficient in the case of
multi-dimensional integrals. However this case is particularly
susceptible to the flaws in random number generators. It is a common
feature that when a random set of coordinates in a 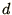 -dimensional
space is generated (i.e. a set of
-dimensional
space is generated (i.e. a set of 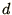 random numbers), the resulting distribution contains (hyper)planes on
which the probability is either significantly higher or lower than
expected.
random numbers), the resulting distribution contains (hyper)planes on
which the probability is either significantly higher or lower than
expected.



Next: The Metropolis Algorithm
Up: Monte Carlo Methods and
Previous: Random Number Generators
![]() when
when ![]() is a random number distributed according to a distribution
is a random number distributed according to a distribution ![]() , then
, then
![]() -dimensional
space is generated (i.e. a set of
-dimensional
space is generated (i.e. a set of ![]() random numbers), the resulting distribution contains (hyper)planes on
which the probability is either significantly higher or lower than
expected.
random numbers), the resulting distribution contains (hyper)planes on
which the probability is either significantly higher or lower than
expected.