


Next: The Ising model
Up: Monte Carlo Methods and
Previous: Monte-Carlo Integration
The Metropolis Algorithm
In statistical mechanics we commonly want to evaluate thermodynamic
averages of the form
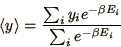 |
(4.10) |
where 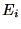 is the energy of the system in state i and
is the energy of the system in state i and
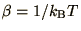 . Such problems can be solved using the
Metropolis et al. (1953) algorithm.
. Such problems can be solved using the
Metropolis et al. (1953) algorithm.
Let us suppose the system is initially in a particular state 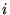 and we
change it to another state
and we
change it to another state 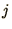 . The detailed balance condition
demands that in equilibrium the flow from
. The detailed balance condition
demands that in equilibrium the flow from 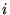 to
to 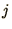 must be balanced by
the flow from
must be balanced by
the flow from 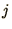 to
to 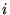 . This can be expressed as
. This can be expressed as
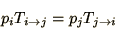 |
(4.11) |
where 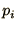 is the probability of finding the system in state i and
is the probability of finding the system in state i and
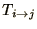 is the probability (or rate) that a system in state i will
make a transition to state j. (4.11) can be rearranged
to read
is the probability (or rate) that a system in state i will
make a transition to state j. (4.11) can be rearranged
to read
Generally the right-hand-side of (4.3) is known and we want
to generate a set of states which obey the distribution 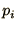 .
This can be achieved by choosing the transition rates such that
.
This can be achieved by choosing the transition rates such that
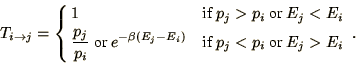 |
(4.14) |
In practice if 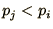 a random number,
a random number, 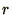 , is chosen between
, is chosen between
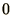 and
and 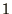 and
the system is moved to state
and
the system is moved to state 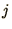 only if
only if 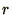 is less than
is less than
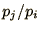 or
or
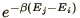 .
.
This method is not the only way in which the
condition
can be fulfilled, but it is by far the most commonly used.
An important feature of the procedure is that it is never necessary to
evaluate the partition function, the denominator in (4.10) but
only the relative probabilities of the different states. This is
usually much easier to achieve as it only requires the calculation of
the change of energy from one state to another.
Note that, although we have derived the algorithm in the context of
thermodynamics, its use is by no means confined to that case. See for
example the quantum Monte-Carlo
methods.
Subsections



Next: The Ising model
Up: Monte Carlo Methods and
Previous: Monte-Carlo Integration
![]() and we
change it to another state
and we
change it to another state ![]() . The detailed balance condition
demands that in equilibrium the flow from
. The detailed balance condition
demands that in equilibrium the flow from ![]() to
to ![]() must be balanced by
the flow from
must be balanced by
the flow from ![]() to
to ![]() . This can be expressed as
. This can be expressed as