


Next: Thermodynamic Averages
Up: The Metropolis Algorithm
Previous: The Metropolis Algorithm
The Ising model
As a simple example of the Metropolis Method we consider the Ising model
of a ferromagnet
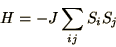 |
(4.15) |
where J is a positive energy,
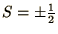 , and i and j are nearest neighbours on a lattice. In this case
we change from one state to another by flipping a single spin and the
change in energy is simply
, and i and j are nearest neighbours on a lattice. In this case
we change from one state to another by flipping a single spin and the
change in energy is simply
 |
(4.16) |
where the sum is only over the nearest neighbours of the flipped spin.
The simulation proceeds by choosing a spin (usually at random) and
testing whether the energy would be increased or decreased by flipping
the spin. If it is decreased
the rules say that the spin should
definitely be flipped. If, on the other hand, the energy is increased,
a uniform random number, 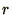 , between
, between 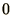 and
and 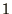 is generated and
compared with
is generated and
compared with
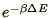 . If it is smaller the spin is
flipped, otherwise the spin is unchanged.
. If it is smaller the spin is
flipped, otherwise the spin is unchanged.
Further information can be found in
the Ising Model project.



Next: Thermodynamic Averages
Up: The Metropolis Algorithm
Previous: The Metropolis Algorithm
![]() , between
, between ![]() and
and ![]() is generated and
compared with
is generated and
compared with
![]() . If it is smaller the spin is
flipped, otherwise the spin is unchanged.
. If it is smaller the spin is
flipped, otherwise the spin is unchanged.