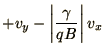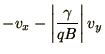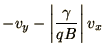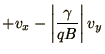Next: The Analytical Solution
Up: A Uniform Field
Previous: A Uniform Field
Note firstly that there are only 2 independent constants in the
problem,
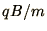 and
and 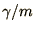 , and that these constants have the units of inverse
time; in fact the former
is the cyclotron frequency and the latter is a damping
rate. In general in any programming problem it pays to think
carefully about the units to be used in the program. There are several
reasons for this.
, and that these constants have the units of inverse
time; in fact the former
is the cyclotron frequency and the latter is a damping
rate. In general in any programming problem it pays to think
carefully about the units to be used in the program. There are several
reasons for this.
- If inappropriate units are used the program may not work at all.
An example of this would be the use of SI units to study the dynamics of
galaxies or to study atomic physics. In the former
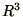 might easily
arise and be bigger than the largest number representable on the
machine, whereas in the latter
might easily
arise and be bigger than the largest number representable on the
machine, whereas in the latter 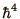 may be smaller than the
smallest number on the machine and be set automatically to zero with
disastrous consequences.
may be smaller than the
smallest number on the machine and be set automatically to zero with
disastrous consequences.
- The problem often has its own natural units and it makes sense to
work in these units. This has the consequence that most of the numbers
in your program will be of order unity rather than very large or very
small.
In general you should look for the natural units of a problem and write
your program appropriately. Note that these will generally not be SI or
cgs.
In the problem we are considering here there are 2 natural time
scales, 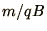 and
and 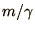 . If we decide to work in one of these,
e.g. the cyclotron period
. If we decide to work in one of these,
e.g. the cyclotron period 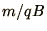 , we can rewrite (1.43) in
the simpler form
, we can rewrite (1.43) in
the simpler form
or perhaps
depending on the sign of 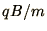 .
Here
.
Here 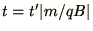 and we have chosen our coordinate
system such that the magnetic field,
and we have chosen our coordinate
system such that the magnetic field, 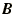 , is in the
, is in the 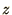 -direction.
Note, in addition, that choosing the units appropriately has eliminated all but
one of the constants from the problem. This cuts down on superfluous
arithmetic in the program.
-direction.
Note, in addition, that choosing the units appropriately has eliminated all but
one of the constants from the problem. This cuts down on superfluous
arithmetic in the program.



Next: The Analytical Solution
Up: A Uniform Field
Previous: A Uniform Field