


Next: The Dufort-Frankel Method
Up: Parabolic Equations
Previous: Parabolic Equations
We consider the diffusion equation and apply the same simple method we
tried for the hyperbolic case.
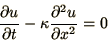 |
(2.26) |
and discretise it using the Euler method for the time derivative and the
simplest centred 2nd order derivative to obtain
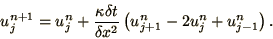 |
(2.27) |
Applying the von Neumann analysis to this system by considering
a single Fourier mode in  space, we obtain
space, we obtain
![\begin{displaymath}
v^{n+1} = v^n\left[
1 - {4\kappa\delta t\over\delta x^2}\sin^2\left(k\delta x\over 2\right)
\right]
\end{displaymath}](img211.png) |
(2.28) |
so that the condition that the method is stable for all 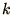 gives
gives
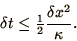 |
(2.29) |
Although the method is in fact conditionally stable the condition
(2.29) hides an uncomfortable property: namely, that if we
want to improve accuracy and allow for smaller wavelengths by halving
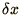 we must divide
we must divide 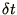 by
by 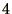 . Hence, the number of space steps is doubled and the number of
time steps is quadrupled: the time required is multiplied by
. Hence, the number of space steps is doubled and the number of
time steps is quadrupled: the time required is multiplied by 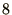 .
Note that this is different from the sorts of conditions we have
encountered up to now, in that it doesn't depend on any real physical time
scale of the problem.
.
Note that this is different from the sorts of conditions we have
encountered up to now, in that it doesn't depend on any real physical time
scale of the problem.



Next: The Dufort-Frankel Method
Up: Parabolic Equations
Previous: Parabolic Equations