


Next: Other Methods
Up: Parabolic Equations
Previous: A Simple Method
We consider here one of many alternative algorithms which have been
designed to overcome the stability problems of the simple algorithm.
The Dufort-Frankel method is a trick which exploits the
unconditional stability of the intrinsic method for simple differential equations.
We modify (2.27) to read
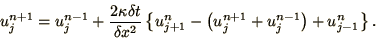 |
(2.30) |
which can be solved explicitly for 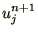 at each mesh point
at each mesh point
 |
(2.31) |
where
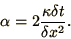 |
(2.32) |
When the usual von Neumann analysis is applied to this method it
is found to be unconditionally stable. Note however that this does not
imply that 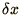 and
and 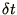 can be made indefinitely large;
common sense tells us that they must be small compared to any real
physical time or length scales in the problem. We must still worry about
the accuracy of the method. Another difficulty this method shares with
the Leap-Frog method
is that it requires boundary conditions at 2 times rather than one, even
though the original diffusion equation is only 1st order in time.
can be made indefinitely large;
common sense tells us that they must be small compared to any real
physical time or length scales in the problem. We must still worry about
the accuracy of the method. Another difficulty this method shares with
the Leap-Frog method
is that it requires boundary conditions at 2 times rather than one, even
though the original diffusion equation is only 1st order in time.



Next: Other Methods
Up: Parabolic Equations
Previous: A Simple Method