


Next: Partial Diagonalisation
Up: Matrix Eigenvalue Problems
Previous: Full Diagonalisation
The Generalised Eigenvalue Problem
A common generalisation of the simple eigenvalue problem involves 2
matrices
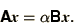 |
(3.29) |
This can easily be transformed into a simple eigenvalue problem by multiplying
both sides by the inverse of either 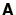 or
or 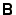 . This has
the disadvantage however that if both matrices are Hermitian
. This has
the disadvantage however that if both matrices are Hermitian
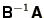 is not, and the advantages of the symmetry are
lost, together, possibly, with some important physics.
There is actually a more efficient way of handling the transformation.
Using Cholesky factorisation an
is not, and the advantages of the symmetry are
lost, together, possibly, with some important physics.
There is actually a more efficient way of handling the transformation.
Using Cholesky factorisation an
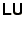 decomposition
of a positive definite matrix can be carried out such that
decomposition
of a positive definite matrix can be carried out such that
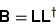 |
(3.30) |
which can be interpreted as a sort of square root of 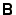 . Using
this we can transform the problem into the form
. Using
this we can transform the problem into the form
Most libraries contain routines for solving the generalised eigenvalue
problem for Hermitian and Real
Symmetric matrices using Cholesky Factorisation
followed by a standard routine. Problem 6 contains a simple
and informative example.



Next: Partial Diagonalisation
Up: Matrix Eigenvalue Problems
Previous: Full Diagonalisation
![$\displaystyle \left[\bss{L}^{-1}\bss{A}\left(\bss{L}^\dagger\right)^{-1}\right]
\left[\bss{L}^\dagger \bi{x}\right]$](img444.png)