


Next: The Gauss-Seidel Method
Up: Iterative Methods
Previous: Iterative Methods
We first divide the matrix 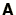 into 3
parts
into 3
parts
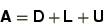 |
(3.13) |
where 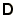 is a diagonal matrix (i.e.
is a diagonal matrix (i.e. 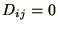 for
for 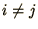 )
and
)
and 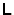 and
and 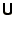 are strict lower and upper
triangular matrices respectively (i.e.
are strict lower and upper
triangular matrices respectively (i.e.
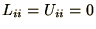 for all
for all 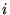 ).
We now write the Jacobi or Gauss-Jacobi iterative procedure to solve our system of equations as
).
We now write the Jacobi or Gauss-Jacobi iterative procedure to solve our system of equations as
![\begin{displaymath}
\bss{X}^{n+1} = \bss{D}^{-1}\left[\bss{B} - \left(\bss{L} +
\bss{U}\right)\bss{X}^n\right]
\end{displaymath}](img406.png) |
(3.14) |
where the superscripts 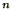 refer to the iteration number.
Note that in practice this procedure requires the storage of the
diagonal matrix,
refer to the iteration number.
Note that in practice this procedure requires the storage of the
diagonal matrix, 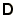 , and a function to multiply the vector,
, and a function to multiply the vector,
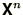 by
by
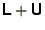 .
This algorithm resembles the
iterative solution of hyperbolic or parabolic partial differential equations, and can be
analysed in the same spirit. In particular care must be taken that the
method is stable.
Simple C
code to implement this for a 1D Poisson's equation is
given below.
.
This algorithm resembles the
iterative solution of hyperbolic or parabolic partial differential equations, and can be
analysed in the same spirit. In particular care must be taken that the
method is stable.
Simple C
code to implement this for a 1D Poisson's equation is
given below.
int i;
const int N = ??; // incomplete code
double xa[N], xb[N], b[N];
while ( ... ) // incomplete code
{
for ( i = 0; i < N; i++ )
xa[i] = (b[i] - xb[i-1] - xb[i+1]) * 0.5;
for ( i = 0; i < N; i++ )
xb[i] = xa[i];
}
Note that 2 arrays are required for X and that the matrices,
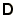 ,
, 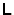 and
and 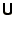 don't appear explicitely.
don't appear explicitely.



Next: The Gauss-Seidel Method
Up: Iterative Methods
Previous: Iterative Methods