


Next: Matrix Eigenvalue Problems
Up: Iterative Methods
Previous: The Jacobi Method
Any implementation of the
Jacobi Method
above will involve a loop over
the matrix elements in each column of 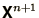 . Instead of
calculating a completely new matrix
. Instead of
calculating a completely new matrix 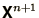 at each iteration and
then replacing
at each iteration and
then replacing 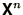 with it before the next iteration,
as in the above code, it might
seem sensible to replace the elements of
with it before the next iteration,
as in the above code, it might
seem sensible to replace the elements of 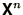 with those of
with those of
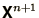 as soon as they have been calculated. Naïvely we
would expect faster convergence. This is equivalent to rewriting the
Jacobi equation as
as soon as they have been calculated. Naïvely we
would expect faster convergence. This is equivalent to rewriting the
Jacobi equation as
![\begin{displaymath}
\bss{X}^{n+1} = \left(\bss{D} + \bss{L}\right)^{-1}\left[\bss{B} -
\bss{U}\bss{X}^n\right].
\end{displaymath}](img410.png) |
(3.15) |
This Gauss-Seidel method has better convergence than the Jacobi
method, but only marginally so.
As before we consider the example of the solution of the 1D Poisson's
equation. As C
programs the basic structure might be something
like
int i;
const int N = ??; //incomplete code
double x[N], b[N];
while ( ... ) //incomplete code
{
for ( i = 0; i < N; i++ )
x[i] = (b[i] - x[i-1] - x[i+1]) * 0.5;
}
Note that only one array is now required to store X, whereas the
Jacobi method needed 2.
The time required for each iteration is proportional to 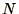 for each
column of
for each
column of 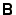 , assuming
, assuming 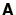 is
sparse.
The number of iterations required depends on the
details of the problem, on the quality of the initial guess for
is
sparse.
The number of iterations required depends on the
details of the problem, on the quality of the initial guess for
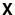 , and on the accuracy of the required solution.
, and on the accuracy of the required solution.



Next: Matrix Eigenvalue Problems
Up: Iterative Methods
Previous: The Jacobi Method