


Next: Full Diagonalisation
Up: Matrix Eigenvalue Problems
Previous: Schrödinger's equation
The usual form of the eigenvalue problem is written
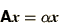 |
(3.26) |
where 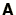 is a square matrix
is a square matrix 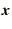 is an
eigenvector and
is an
eigenvector and 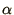 is an eigenvalue. Sometimes the
eigenvalue and eigenvector are called latent root and
latent vector respectively. An
is an eigenvalue. Sometimes the
eigenvalue and eigenvector are called latent root and
latent vector respectively. An 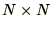 matrix usually has
matrix usually has 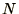 distinct eigenvalue/eigenvector pairs3.2.
The full solution of the eigenvalue problem can then be written in the
form
distinct eigenvalue/eigenvector pairs3.2.
The full solution of the eigenvalue problem can then be written in the
form
where
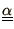 is a
diagonal
matrix of
eigenvalues and
is a
diagonal
matrix of
eigenvalues and 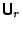 (
(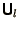 ) are matrices whose columns
(rows) are the corresponding eigenvectors.
) are matrices whose columns
(rows) are the corresponding eigenvectors. 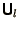 and
and 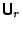 are the left and right handed eigenvectors
respectively, and
are the left and right handed eigenvectors
respectively, and
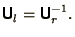 3.3
3.3
- For Hermitian matrices
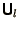 and
and
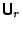 are unitary and are therefore
Hermitian transposes of each other:
are unitary and are therefore
Hermitian transposes of each other:
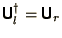 .
.
- For Real Symmetric matrices
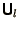 and
and 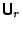 are also real. Real unitary matrices are sometimes
called orthogonal.
are also real. Real unitary matrices are sometimes
called orthogonal.



Next: Full Diagonalisation
Up: Matrix Eigenvalue Problems
Previous: Schrödinger's equation