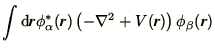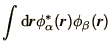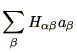Next: General Principles
Up: Matrix Eigenvalue Problems
Previous: Matrix Eigenvalue Problems
Schrödinger's equation
In dimensionless form the time-independent Schrödinger equation can
be written as
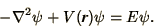 |
(3.16) |
The Laplacian, 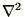 , can be represented in discrete form as in the
case of
Laplace's or Poisson's equations. For example, in 1D (3.16)
becomes
, can be represented in discrete form as in the
case of
Laplace's or Poisson's equations. For example, in 1D (3.16)
becomes
 |
(3.17) |
which can in turn be written in terms of a tridiagonal matrix 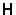 as
as
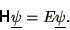 |
(3.18) |
An alternative and more common procedure is to represent the
eigenfunction in terms of a linear combination of basis
functions so that we have
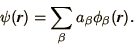 |
(3.19) |
The basis functions are usually chosen for convenience and as some
approximate analytical solution of the problem. Thus in chemistry it is
common to choose the 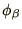 to be known atomic orbitals. In
solid state physics often plane waves are chosen.
Inserting (3.19) into (3.16) gives
to be known atomic orbitals. In
solid state physics often plane waves are chosen.
Inserting (3.19) into (3.16) gives
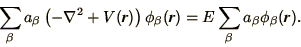 |
(3.20) |
Multiplying this by one of the 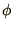 's and integrating
gives
's and integrating
gives
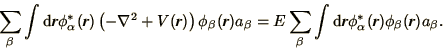 |
(3.21) |
We now define 2 matrices
so that the whole problem can be written concisely as
which has the form of the
generalised eigenvalue problem. Often the
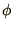 's are chosen to be orthogonal so that
's are chosen to be orthogonal so that
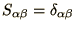 and the matrix
and the matrix 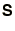 is eliminated from the
problem.
is eliminated from the
problem.



Next: General Principles
Up: Matrix Eigenvalue Problems
Previous: Matrix Eigenvalue Problems