| (4.20) | |||
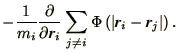 |
(4.21) |
| (4.20) | |||
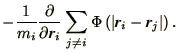 |
(4.21) |
A common feature of such problems is that the time derivative of one
variable only involves the other variable as with ![]() and
and ![]() in the above equations of motion. In such circumstances a leap-frog like method suggests
itself as the most appropriate. Hence we write
in the above equations of motion. In such circumstances a leap-frog like method suggests
itself as the most appropriate. Hence we write
| (4.22) | |||
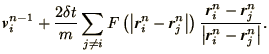 |
(4.23) |
The temperature is defined from the kinetic energy of N particles via
As an example of another thermodynamic quantity consider the specific
heat at constant volume ![]() . This can be calculated by changing the
total energy by multiplying all the velocities by a constant amount
(
. This can be calculated by changing the
total energy by multiplying all the velocities by a constant amount
(
![]() ) and running for some
time to determine the temperature. Note that, as the temperature is
defined in terms of a time average, multiplying all the velocities
by
) and running for some
time to determine the temperature. Note that, as the temperature is
defined in terms of a time average, multiplying all the velocities
by ![]() does
not necessarily imply a simple change of temperature,
does
not necessarily imply a simple change of temperature,
![]() . At a 1st order phase transition, for example, the system might
equilibrate to the same temperature as before with the additional energy
contributing to the latent heat.
. At a 1st order phase transition, for example, the system might
equilibrate to the same temperature as before with the additional energy
contributing to the latent heat.
When the specific heat is known for a range of temperatures it becomes
possible, at least in principle, to calculate the entropy from the
relationship
The pressure is rather more tricky as it is defined in terms of the free
energy, ![]() , using
, using
It is also possible to define modified equations of motion which, rather than conserving energy and volume, conserve temperature or pressure. These are useful for describing isothermal or isobaric processes.
Note that for a set of mutually attractive particles it may not be necessary to constrain the volume but for mutually repulsive particles it certainly is necessary.