


Next: Project The
Up: Monte Carlo Methods and
Previous: General Principles
Problems
- Show that (4.1) has the property that it generates
all
the integers from
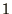 to
to 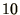 in an apparently random order if
in an apparently random order if 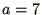 and
and
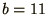 , and that the sequence repeats itself thereafter.
, and that the sequence repeats itself thereafter.
- A certain statistical quantity is distributed
according to
Given a function which generates random numbers uniformly distributed
between 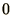 &
& 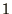 , show how to transform these into the distribution
, show how to transform these into the distribution
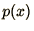 .
.
- Suggest a Monte-Carlo integration procedure for
the integral
- Describe how you would use the Metropolis algorithm to
generate a set of random numbers distributed according to the integrand
of problem 3.
The following are essay type questions which are provided as
examples of the sorts of questions which might arise in an examination
of Monte-Carlo and related methods.
- In an ionic conductor, such as
 , there are several places available on the lattice for
each
, there are several places available on the lattice for
each 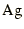 ion, and the ions can move relatively easily between
these sites, subject to the Coulomb repulsion between the ions.
Describe how you would use the Metropolis algorithm to
simulate such a system.
ion, and the ions can move relatively easily between
these sites, subject to the Coulomb repulsion between the ions.
Describe how you would use the Metropolis algorithm to
simulate such a system.
- Some quantum mechanics textbooks suggest that the
ground state wave function for a Hydrogen atom is
Describe how you would use the variational quantum Monte-Carlo
procedure to calculate the ground state energy for a range of values of
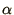 and hence how you would provide estimates of the true ground
state energy and the value of
and hence how you would provide estimates of the true ground
state energy and the value of 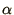 .
.
- Describe how you would simulate the melting (or
sublimation) of Argon in vacuo using the molecular dynamics
method. Pay particular attention to how you would calculate the
specific and latent heats.



Next: Project The
Up: Monte Carlo Methods and
Previous: General Principles