


Next: The Physics
Up: Project The
Previous: Introduction
Here we will consider the simple case of a 2 dimensional
square lattice with interactions only between nearest neighbours. In
this case
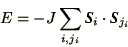 |
(4.28) |
where 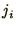 is only summed over the 4 nearest neighbours of
is only summed over the 4 nearest neighbours of 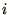 .
.
This model can be studied using the Metropolis method as described in
the notes, where the state can be changed by flipping a single spin.
Note that the change in energy due to flipping the 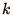 th spin from
th spin from
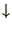 to
to  is given by
is given by
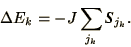 |
(4.29) |
The only quantity which actually occurs in the calculation is
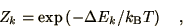 |
(4.30) |
and this can only take one of five different values given by the number
of neighbouring  spins. Hence it is sensible to store these
in a short array before starting the calculation. Note also that there
is really only 1 parameter in the model,
spins. Hence it is sensible to store these
in a short array before starting the calculation. Note also that there
is really only 1 parameter in the model, 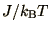 , so that it would
make sense to write your program in terms of this single parameter
rather than
, so that it would
make sense to write your program in terms of this single parameter
rather than 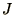 and
and 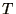 separately.
separately.
The calculation should use periodic boundary conditions, in order to
avoid spurious effects due to boundaries.
There are several different ways to achieve this. One of the most efficient
is to think of the system as a single line of spins wrapped round a
torus. This way it is possible to avoid a lot of checking for the
boundary. For an 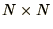 system of spins
define an array of
system of spins
define an array of 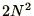 elements using the shortest sensible variable
type: char in C(++). It is easier to use
elements using the shortest sensible variable
type: char in C(++). It is easier to use 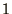 for spin
for spin  and
and 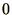 for spin
for spin  , as this makes the
calculation of the number of neighbouring
, as this makes the
calculation of the number of neighbouring  spins easier. In
order to map between spins in a 2d space
spins easier. In
order to map between spins in a 2d space  and in the 1d
array
and in the 1d
array 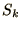 the following mapping can be used.
the following mapping can be used.
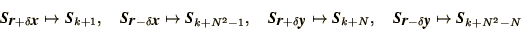 |
(4.31) |
where the 2nd 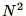 elements of the array are always maintained equal to
the 1st
elements of the array are always maintained equal to
the 1st 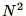 .
This way it is never necessary to check whether one of the neighbours is
over the edge. It is important to remember to change
.
This way it is never necessary to check whether one of the neighbours is
over the edge. It is important to remember to change
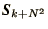 whenever
whenever 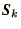 is changed.
is changed.
The calculation proceeds as follows:
- Initialise the spins, either randomly or aligned.
- Choose a spin to flip. It is better to choose a
spin at random rather than systematically as systematic choices can lead
to spurious temperature gradients across the system.
- Decide whether to flip the spin by using the Metropolis condition
(see notes).
- If the spin is to be flipped, do so but remember to flip its mirror
in the array.
- Update the energy and magnetisation.
- Add the contributions to the required averages.
- Return to step 2 and repeat.



Next: The Physics
Up: Project The
Previous: Introduction
![]() th spin from
th spin from
![]() to
to ![]() is given by
is given by
![]() system of spins
define an array of
system of spins
define an array of ![]() elements using the shortest sensible variable
type: char in C(++). It is easier to use
elements using the shortest sensible variable
type: char in C(++). It is easier to use ![]() for spin
for spin ![]() and
and ![]() for spin
for spin ![]() , as this makes the
calculation of the number of neighbouring
, as this makes the
calculation of the number of neighbouring ![]() spins easier. In
order to map between spins in a 2d space
spins easier. In
order to map between spins in a 2d space ![]() and in the 1d
array
and in the 1d
array ![]() the following mapping can be used.
the following mapping can be used.