


Next: Project Quantum
Up: Project The
Previous: The Model and Method
In general it is advisable to run the program for some time to allow it
to reach equilibrium before trying to calculate any averages. Close to
a phase transition it is often necessary to run for much longer to
reach equilibrium. The behaviour of the total energy during the run is
usually a good guide to whether equilibrium has been reached.
The total energy, 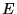 , and the magnetisation can be calculated from
(4.27) and
, and the magnetisation can be calculated from
(4.27) and
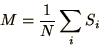 |
(4.32) |
It should be possible to calculate these as you go along, by
accumulating the changes rather than
by recalculating the complete sum after each step.
A 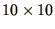 lattice should suffice for most purposes and certainly
for testing, but you may require a much bigger lattice close to a
transition.
lattice should suffice for most purposes and certainly
for testing, but you may require a much bigger lattice close to a
transition.
A useful trick is to use the final state at one temperature as the
initial state for the next slightly different temperature. That way the
system won't need so long to reach equilibrium.
It should be possible to calculate the specific heat and the
magnetic susceptibility. The specific heat could be calculated by
differentiating the energy with respect to temperature. This is a
numerically questionable procedure however. Much better is to use the
relationship
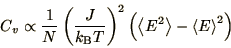 |
(4.33) |
Similarly, in the paramagnetic state, the susceptibility can be
calculated using
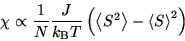 |
(4.34) |
where
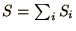 and the averages are over different states, i.e.
can be calculated by averaging over the different Metropolis steps.
Both these quantities are expected to diverge at the transition, but
the divergence will tend to be rounded off due to the small size of the
system. Note however that the fact that (4.33) &
(4.34) have the form of variances, and that these diverge at the
transition, indicates that the average energy and magnetisation will be
subject to large fluctuations around the transition.
and the averages are over different states, i.e.
can be calculated by averaging over the different Metropolis steps.
Both these quantities are expected to diverge at the transition, but
the divergence will tend to be rounded off due to the small size of the
system. Note however that the fact that (4.33) &
(4.34) have the form of variances, and that these diverge at the
transition, indicates that the average energy and magnetisation will be
subject to large fluctuations around the transition.
Finally a warning. A common error made in such calculations is to add a
contribution to the averages only when a spin is flipped. In fact this
is wrong as the fact that it isn't flipped means that the original state
has a higher probability of occupation.



Next: Project Quantum
Up: Project The
Previous: The Model and Method