


Next: Problems
Up: Ordinary Differential Equations
Previous: The Intrinsic Method
Summary
In these notes we have introduced some methods for solving ordinary
differential equations. However, by far the most important lesson to be
learned is that to be useful a method must be both accurate and
stable. The latter condition is often the most difficult to
fulfil and careful analysis of the equations to be solved may be
necessary before choosing an appropriate method to use for finding a
numerical solution.
The stability conditions derived above tend to have the form
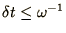 which may be interpreted as
which may be interpreted as 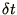 should be less
than the characteristic period of oscillation. This conforms with
common sense. In fact we can write down a more general common sense
condition:
should be less
than the characteristic period of oscillation. This conforms with
common sense. In fact we can write down a more general common sense
condition: 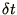 should be small compared with the smallest time
scale present in the problem.
Finally, many realistic problems don't fall into the neat categories of
(1.1). The simplest example is a damped harmonic oscillator.
Often it is difficult to find an exact analytical solution
for the stability condition. It pays in such cases to consider some
extreme conditions, such as (e.g. ) very weak damping or very strong
damping, work out the conditions for these cases and simply choose the
most stringent condition. In non-linear problems the cases when the
unknown,
should be small compared with the smallest time
scale present in the problem.
Finally, many realistic problems don't fall into the neat categories of
(1.1). The simplest example is a damped harmonic oscillator.
Often it is difficult to find an exact analytical solution
for the stability condition. It pays in such cases to consider some
extreme conditions, such as (e.g. ) very weak damping or very strong
damping, work out the conditions for these cases and simply choose the
most stringent condition. In non-linear problems the cases when the
unknown, 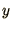 , is very large or very small may provide tractable
solutions.
, is very large or very small may provide tractable
solutions.



Next: Problems
Up: Ordinary Differential Equations
Previous: The Intrinsic Method