


Next: Summary
Up: Ordinary Differential Equations
Previous: The Predictor-Corrector Method
The Intrinsic Method
Returning to the possibility of solving the integral equation using the trapezoidal or
trapezium rule,
let us consider the case of a
linear differential equation, such as our examples. For the decay equation we have
![\begin{displaymath}
y_{n+1} = y_n - {\mathchoice{{\textstyle{\frac12}}}{{\texts...
...style{1/2}}}}\delta t\left[\alpha y_{n+1} + \alpha y_n\right]
\end{displaymath}](img111.png) |
(1.41) |
which can be rearranged into an explicit equation for 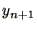 as a function
of
as a function
of 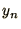
![\begin{displaymath}
y_{n+1} = \left[ 1 - {\mathchoice{{\textstyle{\frac12}}}{{\...
...{{\scriptscriptstyle{1/2}}}}\delta t\cdot \alpha \right] y_n.
\end{displaymath}](img112.png) |
(1.42) |
This intrinsic method is 2nd order accurate as that is the
accuracy of the trapezoidal rule for integration. What about the
stability? Applying the same methodology as before we find that the
crucial quantity, 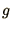 , is the expression in square brackets,
, is the expression in square brackets, ![$[]$](img51.png) , in
(1.42) which is always
, in
(1.42) which is always 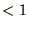 for the decay equation and
has modulus unity in the oscillatory case (after
substituting
for the decay equation and
has modulus unity in the oscillatory case (after
substituting
 ). Hence it is stable in both
cases. Why is it not used instead of the other methods? Unfortunately
only a small group of equations, such as our examples, can be rearranged
in this way. For non-linear equations it may be impossible, and even
for linear equations when
). Hence it is stable in both
cases. Why is it not used instead of the other methods? Unfortunately
only a small group of equations, such as our examples, can be rearranged
in this way. For non-linear equations it may be impossible, and even
for linear equations when 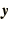 is a vector, there may be a formal
solution which is not useful in practice. It is always possible to solve
the resulting non-linear equation iteratively, using (e.g. )
Newton-Raphson iteration, but this is usually not worthwhile in
practice.
In fact the intrinsic method is also stable for the growth equation when
it is analysed as discussed earlier, so that the method is in fact stable for all
3 classes of equations.
is a vector, there may be a formal
solution which is not useful in practice. It is always possible to solve
the resulting non-linear equation iteratively, using (e.g. )
Newton-Raphson iteration, but this is usually not worthwhile in
practice.
In fact the intrinsic method is also stable for the growth equation when
it is analysed as discussed earlier, so that the method is in fact stable for all
3 classes of equations.
| Decay |
Growth |
Oscillation |
| stable |
stable |
stable |



Next: Summary
Up: Ordinary Differential Equations
Previous: The Predictor-Corrector Method