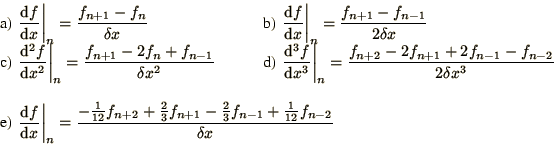Next: Project Classical
Up: Ordinary Differential Equations
Previous: Summary
Problems
- Write down definitions of the terms order of accuracy,
truncation error, conditional stability as applied to
the numerical solution of ordinary differential equations.
- Write down 1st order accurate finite difference approximations for
Hint: the result has to be something like
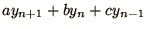 . Expand the
. Expand the 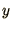 s around
s around 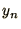 and choose the coefficients to
eliminate contributions from unwanted terms in the expansion.
N.B. This question refers to the accuracy of the approximation for
the derivatives given, not to the accuracy of
and choose the coefficients to
eliminate contributions from unwanted terms in the expansion.
N.B. This question refers to the accuracy of the approximation for
the derivatives given, not to the accuracy of 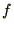 .
.
- Derive expressions for the truncation error of the following
difference approximations.
- The torsion of a bar is described by the differential equation
Show how to re-express this as a system of first order differential
equations.
- Write down an expression for solving the
differential equation
by Euler's method and show under what conditions the method is stable.
Write and test a short program (it should only require a few lines) to
test the method. Vary 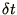 ,
, 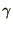 and
and 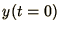 to check the
validity of the stability condition you have derived.
to check the
validity of the stability condition you have derived.
- Using equation 1.2.5 show that the
Euler method is
stable for a vector equation provided all the eigenvalues of
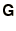 have modulus less than or equal to unity.
have modulus less than or equal to unity.
- Show that equation 1.37 gives the
correct stability condition for both the Runge-Kutta and
Predictor-Corrector methods. Why do you think this is a good method
for damped oscillatory equations? (The last part doesn't have to be
mathematically rigorous).



Next: Project Classical
Up: Ordinary Differential Equations
Previous: Summary