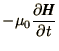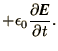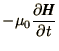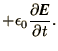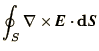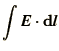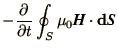Next: Dispersion
Up: Conservative Methods
Previous: The Diffusion Equation
Let us now try to apply the same ideas to Maxwell's equations.
In free space we have
In order to reverse the derivation of these equations we consider space
to be divided into cubes as before. For (2.6.3a) we
integrate over a face of the cube and apply Stokes' theorem
and the integral of the electric field, 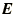 , round the edges of the
face is equal to minus the rate of change of the magnetic flux through
the face, i.e. Faraday's law. Here we can associate the electric field,
, round the edges of the
face is equal to minus the rate of change of the magnetic flux through
the face, i.e. Faraday's law. Here we can associate the electric field,
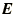 with the edges and the magnetic field with the face of the
cube.
In the case of the diffusion equation we had to think in terms of the
total charge in a cube instead of the density. Now we replace
the electric field with the integral of the field along a line and the
magnetic field with the flux through a face.
Note also that we can analyse (2.6.3b) in a similar way to
obtain a representation of Ampère's law.
with the edges and the magnetic field with the face of the
cube.
In the case of the diffusion equation we had to think in terms of the
total charge in a cube instead of the density. Now we replace
the electric field with the integral of the field along a line and the
magnetic field with the flux through a face.
Note also that we can analyse (2.6.3b) in a similar way to
obtain a representation of Ampère's law.



Next: Dispersion
Up: Conservative Methods
Previous: The Diffusion Equation