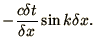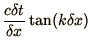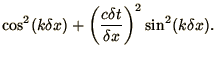Next: Problems
Up: Partial Differential Equations
Previous: Maxwell's Equations
Dispersion
Let us return to the Lax method
for hyperbolic equations. The solution of the differential equation has
the form
 |
(2.42) |
where 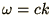 . Let us substitute (2.42) into the Lax
algorithm
. Let us substitute (2.42) into the Lax
algorithm
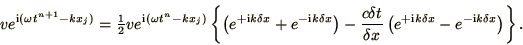 |
(2.43) |
By cancelling the common factors we now obtain
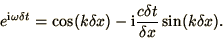 |
(2.44) |
From this we can derive a dispersion relation,
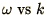 , for the
discrete equation and compare the result with
, for the
discrete equation and compare the result with 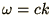 for the
original differential equation. Since,
in general,
for the
original differential equation. Since,
in general, 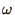 could be complex we write it as
could be complex we write it as
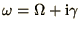 and compare real and imaginary parts on both sides of the equation
to obtain
and compare real and imaginary parts on both sides of the equation
to obtain
Taking the ratio of these or the sum of their squares respectively leads
to the equations
The first of these equations tells us that in general the phase velocity is not
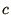 , although for long wavelengths,
, although for long wavelengths,
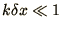 and
and
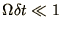 , we recover the
correct dispersion relationship. This is similar to the situation when
we compare lattice vibrations with classical elastic waves: the long
wavelength sound waves are OK but the shorter wavelengths
deviate.
The second equation (2.7b) describes the damping of the
modes. Again for small
, we recover the
correct dispersion relationship. This is similar to the situation when
we compare lattice vibrations with classical elastic waves: the long
wavelength sound waves are OK but the shorter wavelengths
deviate.
The second equation (2.7b) describes the damping of the
modes. Again for small 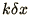 and
and
 ,
, 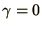 ,
but (e.g.) short
wavelengths,
,
but (e.g.) short
wavelengths,
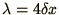 , are strongly damped. This may be a
desirable property as short wavelength oscillations may be spurious.
After all we should have chosen
, are strongly damped. This may be a
desirable property as short wavelength oscillations may be spurious.
After all we should have chosen 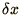 to be small compared with any
expected features. Nevertheless with this particular algorithm
to be small compared with any
expected features. Nevertheless with this particular algorithm
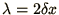 is not damped. Other algorithms, such as Lax-Wendroff,
have been designed specifically to damp anything with a
is not damped. Other algorithms, such as Lax-Wendroff,
have been designed specifically to damp anything with a
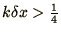 .
.



Next: Problems
Up: Partial Differential Equations
Previous: Maxwell's Equations