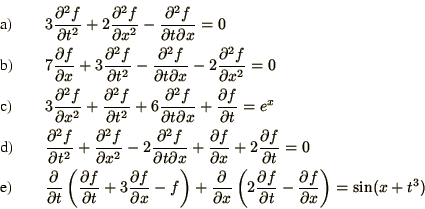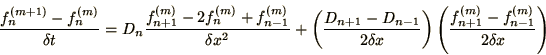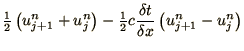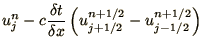Next: Project Lagrangian
Up: Partial Differential Equations
Previous: Dispersion
Problems
- Explain the difference between hyperbolic, parabolic and elliptic
partial differential equations, and give an example of each. What is
the important physical distinction between hyperbolic and parabolic
equations, on the one hand, and elliptic equations on the other?
- Describe the von Neumann procedure for analysing the stability of
partial differential equations.
- Describe the physical principle behind the
Courant-Friedrichs-Lewy condition as applied to the numerical solution
of partial differential equations.
- Are the following equations hyperbolic, elliptic or parabolic?
- The equation
can be represented by the difference equation
Derive the truncation error of this difference equation.
Write down an alternative difference equation which is 2nd order
accurate in both 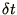 and
and 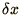 .
.
- The Dufort-Frankel
scheme is a method for the solution of the diffusion equation.
Show that the method is unconditionally stable.
Discuss the advantages and disadvantages of this method.
- The diffusion equation in a medium where the diffusion constant
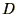 varies in space
varies in space
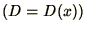 is
is
Show that the difference equation
is not conservative, i.e. 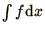 is not conserved.
Construct an alternative difference scheme which is conservative.
is not conserved.
Construct an alternative difference scheme which is conservative.
- Show that the Lax scheme for the
solution of the advection equation is equivalent to
Examine the behaviour of wave-like solutions
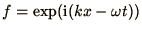 in the Lax scheme and explain the behaviour in terms of diffusion.
in the Lax scheme and explain the behaviour in terms of diffusion.
- Describe what is meant by numerical dispersion.
- Lax-Wendroff method consists of 2 steps, just like Runge-Kutta or
Predictor-Corrector. It is given by
Draw a diagram to illustrate the way this algorithm operates on an
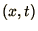 grid.
Show that the algorithm is stable provided the Courant-Friedrichs-Lewy
condition is obeyed.
Show that the algorithm tends to dampen waves with wavelength
grid.
Show that the algorithm is stable provided the Courant-Friedrichs-Lewy
condition is obeyed.
Show that the algorithm tends to dampen waves with wavelength
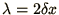 .
.



Next: Project Lagrangian
Up: Partial Differential Equations
Previous: Dispersion