The Growth Equation

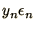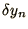Actually, our analysis doesn't make too much sense in the case of the growth equation as the true solution should grow anyway. A more sensible condition would be that the relative error in the solution does not grow. This can be achieved by substituting $y_n \epsilon_n$ for $\delta y_n$ above and looking for the condition that 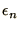$\epsilon_n$ does not grow. We will not treat this case further here but it is, in fact, very important in problems such as chaos, in which small changes in the initial conditions lead to solutions which diverge from one another.