


Next: The Growth Equation
Up: Euler Method
Previous: Order of Accuracy
Stability
The Euler method is 1st order accurate. However there is another
important consideration in analysing the method: stability. Let us
suppose that at some time the actual numerical solution deviates from
the true solution of the difference equation (1.11)
(N.B. not the original differential equation
(1.7)) by some small amount 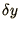 , due, for example, to
the finite accuracy of the computer. Then adding this into
(1.11) gives
, due, for example, to
the finite accuracy of the computer. Then adding this into
(1.11) gives
![\begin{displaymath}
y_{n+1} + \delta y_{n+1}
= y_n + \delta y_n
- \delta t \l...
...ft.\partial f\over\partial y\right\vert _n \delta y_n\right],
\end{displaymath}](img50.png) |
(1.17) |
where the term in brackets, ![$[]$](img51.png) , is the Taylor expansion of
, is the Taylor expansion of 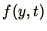 with respect to
with respect to 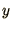 .
Subtracting (1.11) we obtain a linear equation for
.
Subtracting (1.11) we obtain a linear equation for
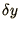
![\begin{displaymath}
\delta y_{n+1} = \left[1 -
\delta t \left.\partial f\over\partial y\right\vert _n\right] \delta y_n ,
\end{displaymath}](img53.png) |
(1.18) |
which it is convenient to write in the form
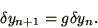 |
(1.19) |
If 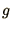 has a magnitude greater than
one then
has a magnitude greater than
one then 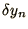 will tend to grow with increasing
will tend to grow with increasing 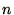 and may
eventually dominate over the required solution. Hence the Euler method
is stable only if
and may
eventually dominate over the required solution. Hence the Euler method
is stable only if 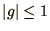 or
or
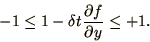 |
(1.20) |
As 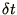 is positive by definition the 2nd inequality implies that
the derivative must also be positive. The 1st inequality leads to a
restriction on
is positive by definition the 2nd inequality implies that
the derivative must also be positive. The 1st inequality leads to a
restriction on 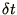 , namely
, namely
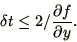 |
(1.21) |
When the derivative is complex more care is required in the calculation
of 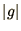 . In this case it is easier to look for solutions of the
condition
. In this case it is easier to look for solutions of the
condition 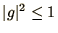 . For the oscillation equation (1.1c)
the condition becomes
. For the oscillation equation (1.1c)
the condition becomes
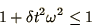 |
(1.22) |
which is impossible to fulfil for real 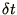 and
and 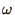 .
Comparing these result with our 3 types of differential equations
(1.1) we find the following stability conditions
.
Comparing these result with our 3 types of differential equations
(1.1) we find the following stability conditions
| Decay |
Growth |
Oscillation |
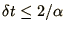 |
unstable |
unstable |
The Euler method is conditionally stable for the decay equation.
A method is stable if a small deviation from the true solution does
not tend to grow as the solution is iterated.



Next: The Growth Equation
Up: Euler Method
Previous: Order of Accuracy