


Next: Application to Vector Equations
Up: Euler Method
Previous: The Growth Equation
Application to Non-Linear Differential Equations
The linear-differential equations in physics can often be solved
analytically whereas most non-linear ones can only be solved
numerically. It is important therefore to be able to apply the ideas
developed here to such cases.
Consider the simple example
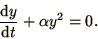 |
(1.23) |
In this case
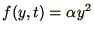 and
and
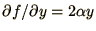 which can be substituted into
(1.21) to give the stability condition
which can be substituted into
(1.21) to give the stability condition
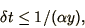 |
(1.24) |
which depends on 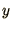 , unlike the simpler cases. In writing a program to
solve such an equation it may therefore be necessary to monitor the
value of the solution,
, unlike the simpler cases. In writing a program to
solve such an equation it may therefore be necessary to monitor the
value of the solution, 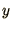 , and adjust
, and adjust 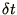 as necessary to
maintain stability.
as necessary to
maintain stability.