


Next: Order of Accuracy
Up: Ordinary Differential Equations
Previous: Types of Differential Equation
Euler Method
Consider an approximate solution of (1.8)
over a small interval
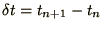 by writing the integral
as
by writing the integral
as
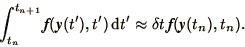 |
(1.10) |
to obtain
or, in a more concise notation,
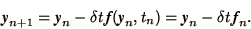 |
(1.11) |
We can integrate over any larger interval by subdividing the range into
sections of width 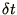 and repeating (1.11) for each
part.
Equivalently we can consider that we have approximated the derivative
with a forward difference
and repeating (1.11) for each
part.
Equivalently we can consider that we have approximated the derivative
with a forward difference
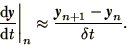 |
(1.12) |
We will also come across centred and backward differences,
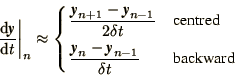 |
(1.13) |
respectively.
Here we have used a notation which is very common in computational
physics, in which we calculate
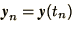 at discrete
values of
at discrete
values of 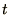 given by
given by
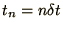 , and
, and
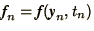 .
In what follows we will drop the vector notation
.
In what follows we will drop the vector notation 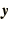 except when it
is important for the discussion.
except when it
is important for the discussion.
Subsections



Next: Order of Accuracy
Up: Ordinary Differential Equations
Previous: Types of Differential Equation