


Next: Molecular Dynamics
Up: Monte Carlo Methods and
Previous: Thermodynamic Averages
Quantum Monte-Carlo
The term Quantum Monte-Carlo does not refer to a particular
method but rather to any method using Monte-Carlo type methods to solve
quantum (usually many-body) problems. As an example consider the
evaluation of the energy of a trial wave function 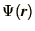 where
where
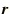 is a 3N dimensional position coordinate of N
particles,
is a 3N dimensional position coordinate of N
particles,
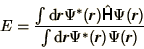 |
(4.17) |
where 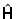 is the Hamiltonian operator. This can be turned
into an appropriate form for Monte-Carlo integration by rewriting as
is the Hamiltonian operator. This can be turned
into an appropriate form for Monte-Carlo integration by rewriting as
![\begin{displaymath}
E = \int\d\bi{r} \left\{\left\vert\Psi(\bi{r})\right\vert^2\...
...right\}
\left[\Psi(\bi{r})^{-1}\hat\bss{H}\Psi(\bi{r})\right]
\end{displaymath}](img577.png) |
(4.18) |
such that the quantity in braces (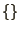 ) has the form of a probability
distribution. This integral can now easily be evaluated by
Monte-Carlo integration. Typically a sequence
of
) has the form of a probability
distribution. This integral can now easily be evaluated by
Monte-Carlo integration. Typically a sequence
of 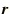 's is generated using the Metropolis algorithm, so that it is not even
necessary to normalise the trial wave function, and the quantity in
square brackets
's is generated using the Metropolis algorithm, so that it is not even
necessary to normalise the trial wave function, and the quantity in
square brackets ![$[]$](img51.png) is averaged over
the
is averaged over
the 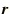 's.
's.
This method, variational quantum Monte-Carlo, presupposes we
have a good guess for the wave function and
want to evaluate an integral over it. It is only one of several
different techniques which are referred to as quantum Monte
Carlo. Others include, Diffusion Monte-Carlo, Green's function
Monte-Carlo and World Line Monte-Carlo.



Next: Molecular Dynamics
Up: Monte Carlo Methods and
Previous: Thermodynamic Averages