


Next: The Predictor-Corrector Method
Up: Ordinary Differential Equations
Previous: The Leap-Frog Method
The Runge-Kutta Method
So far we have found one method which is stable for the decay equation
and another for the oscillatory equation. Can we combine the advantages
of both?
As a possible compromise consider the following two step algorithm
(ignoring vectors)
In practice the intermediate value
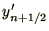 is discarded after
each step.
We see that this method consists of an Euler step followed by a Leap-Frog step.
This is called the 2nd order Runge-Kutta or two-step
method. It is in fact
one of a hierarchy of related methods of different accuracies.
The stability analysis for (1.4) is carried out in the same
way as before. Here we simply quote the result
is discarded after
each step.
We see that this method consists of an Euler step followed by a Leap-Frog step.
This is called the 2nd order Runge-Kutta or two-step
method. It is in fact
one of a hierarchy of related methods of different accuracies.
The stability analysis for (1.4) is carried out in the same
way as before. Here we simply quote the result
![\begin{displaymath}
\delta y_{n+1} = \left[1 - \delta t{\partial f\over\partial...
...ta t {\partial f\over\partial y}\right)^2\right]
\delta y_n.
\end{displaymath}](img104.png) |
(1.37) |
In deriving this result it is necessary to assume that the derivatives,
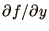 are independent of
are independent of 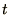 . This is not usually a
problem.
From (1.37) we conclude the stability conditions
. This is not usually a
problem.
From (1.37) we conclude the stability conditions
| Decay |
Growth |
Oscillation |
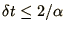 |
unstable |
 |
Note that in the oscillatory case the method is strictly speaking
unstable but the effect is so small that it can be ignored in most
cases, as long as
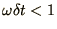 . This method is often used for damped oscillatory equations.
. This method is often used for damped oscillatory equations.



Next: The Predictor-Corrector Method
Up: Ordinary Differential Equations
Previous: The Leap-Frog Method