


Next: The Intrinsic Method
Up: Ordinary Differential Equations
Previous: The Runge-Kutta Method
The Predictor-Corrector Method
This method is very similar to and often confused with the
Runge-Kutta
method. We consider substituting the trapezoidal rule for
the estimate of the integral in (1.8) to obtain the equation
![\begin{displaymath}
\bi{y}_{n+1} = \bi{y}_n - {\mathchoice{{\textstyle{\frac12}...
...[\bi{f}(\bi{y}_{n+1}, t_{n+1}) + \bi{f}(\bi{y}_n,t_n)\right].
\end{displaymath}](img108.png) |
(1.38) |
Unfortunately the presence of 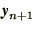 on the right hand side makes
a direct solution of (1.38) impossible except for
special cases. A possible compromise is the following method
on the right hand side makes
a direct solution of (1.38) impossible except for
special cases. A possible compromise is the following method
This method consists of a guess for 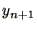 based on the
Euler method (the
Prediction) followed by a correction using the trapezoidal rule
to solve the integral
equation.
The accuracy and stability properties are identical to those of the
Runge-Kutta method.
based on the
Euler method (the
Prediction) followed by a correction using the trapezoidal rule
to solve the integral
equation.
The accuracy and stability properties are identical to those of the
Runge-Kutta method.